
【题目】如图,在正方形ABCD中,E、F分别是边BC、CD上的点,![]() =
=![]() ,CF=DF,连接AE、AF、EF,并延长FE交AB的延长线于点G.
,CF=DF,连接AE、AF、EF,并延长FE交AB的延长线于点G.
(1)若正方形的边长为4,则EG等于 ;
(2)求证:△ECF∽△FDA;
(3)比较∠EAB与∠EAF的大小.

【答案】(1)3![]() ;(2)证明参见解析;(3)∠EAF<∠EAB.
;(2)证明参见解析;(3)∠EAF<∠EAB.
【解析】
试题分析:(1)先根据正方形边长得CF=2,由平行相似得:△FCE∽△GBE,则![]() ,代入求得BG=6,根据勾股定理得:EG=3
,代入求得BG=6,根据勾股定理得:EG=3![]() ;(2)根据已知边的长度分别求
;(2)根据已知边的长度分别求![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,则
,则![]() =
=![]() ,再由正方形性质得:∠C=∠D=90°,则△ECF∽△FDA;(3)先根据(2)中的△ECF∽△FDA,得∠CFE=∠DAF,
,再由正方形性质得:∠C=∠D=90°,则△ECF∽△FDA;(3)先根据(2)中的△ECF∽△FDA,得∠CFE=∠DAF,![]() =
=![]() =
=![]() ,证明∠EFA=90°,分别计算∠EAB与∠EAF的正切值,根据两锐角正切大的角大,得出结论.
,证明∠EFA=90°,分别计算∠EAB与∠EAF的正切值,根据两锐角正切大的角大,得出结论.
试题解析:(1)∵四边形ABCD是正方形,∴AB=CD=BC=4,∠ABC=90°,DC∥AB,∵CF=DF,∴CF=![]() CD=2,
CD=2,
∵DC∥AG,∴△FCE∽△GBE,∴![]() ,∵
,∵![]() =
=![]() ,∴
,∴![]() =
=![]() ,BE=
,BE=![]() BC=
BC=![]() ×4=3,∴
×4=3,∴![]() =
=![]() ,∴BG=6,在Rt△BEG中,EG=
,∴BG=6,在Rt△BEG中,EG=![]() =
=![]() =3
=3![]() ;故答案为:3
;故答案为:3![]() ;(2)∵四边形ABCD是正方形,∴BC=AD=DC=4,∠C=∠D=90°,∵DF=FC=2,CE=1,∴
;(2)∵四边形ABCD是正方形,∴BC=AD=DC=4,∠C=∠D=90°,∵DF=FC=2,CE=1,∴![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴△ECF∽△FDA;(3)∵△ECF∽△FDA,∴∠CFE=∠DAF,
,∴△ECF∽△FDA;(3)∵△ECF∽△FDA,∴∠CFE=∠DAF,![]() =
=![]() =
=![]() ,∵∠DFA+∠DAF=90°,∴∠CFE+∠DFA=90°,∴∠EFA=90°,∴tan∠EAF=
,∵∠DFA+∠DAF=90°,∴∠CFE+∠DFA=90°,∴∠EFA=90°,∴tan∠EAF=![]() =
=![]() ,∵
,∵![]() =
=![]() ,∴tan∠EAB=
,∴tan∠EAB=![]() =
=![]() ,∵
,∵![]() <
<![]() ,∴∠EAF<∠EAB.
,∴∠EAF<∠EAB.


科目:初中数学 来源: 题型:
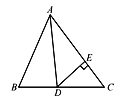
【题目】如图所示,在△ABC中,已知AD是角平分线,∠B=62°,∠C=58°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,小红家阳台上放置了一个晒衣架.如图2是晒衣架的侧面示意图,立杆AB、CD相交于点O,B、D两点立于地面,经测量:AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条直线,且EF=32cm.
(1)求证:AC∥BD;
(2)求扣链EF与立杆AB的夹角∠OEF的度数(精确到0.1°);
(3)小红的连衣裙穿在衣架后的总长度达到122cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.
(参考数据:sin61.9°≈0.882,cos61.9°≈0.471,tan61.9°≈0.553;可使用科学计算器)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A. –2(a–b)=–2a–b B. –2(a–b)=–2a+b
C. –2(a–b)=–2a–2b D. –2(a–b)=–2a+2b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在100米短跑训练中,某5次的平均成绩相等,甲的方差是0.12,乙的方差是0.05,这5次短跑训练成绩较稳定的是_____.(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市教研室对2008年嘉兴市中考数学试题的选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:已知这n人中,平均每题有11人答错,同时第6题答错的人数恰好是第5题答错人数的1.5倍,且第2题有80%的同学答对.则第5题有 人答对.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某礼品制造工厂接受一批玩具的订货任务,按计划天数生产,如果每天生产 20 个玩具,则比订货任务少 100 个;如果每天生产 23 个玩具,则可以超过订货任务 20 个,请求出这批玩具的订货任务是多少个,原计划几天完成任务.
A. 40,800 B. 40,900 C. 50,800 D. 50,900
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com