
【题目】如图,在以线段AB为直径的⊙O上取一点,连接AC、BC.将△ABC沿AB翻折后得到△ABD.
(1)试说明点D在⊙O上;
(2)在线段AD的延长线上取一点E,使AB2=AC·AE.求证:BE为⊙O的切线;
(3)在(2)的条件下,分别延长线段AE、CB相交于点F,若BC=2,AC=4,求线段EF的长.
【答案】(1)证明见解析;(2)证明见解析;(3)EF=![]()
【解析】(1)由翻折知△ABC≌△ABD,得∠ADB=∠C=90°,据此即可得;
(2)由AB=AD知AB2=ADAE,即![]() ,据此可得△ABD∽△AEB,即可得出∠ABE=∠ADB=90°,从而得证;
,据此可得△ABD∽△AEB,即可得出∠ABE=∠ADB=90°,从而得证;
(3)由![]() 知DE=1、BE=
知DE=1、BE=![]() ,证△FBE∽△FAB得
,证△FBE∽△FAB得![]() ,据此知FB=2FE,在Rt△ACF中根据AF2=AC2+CF2可得关于EF的一元二次方程,解之可得.
,据此知FB=2FE,在Rt△ACF中根据AF2=AC2+CF2可得关于EF的一元二次方程,解之可得.
(1)∵AB为⊙O的直径,
∴∠C=90°,
∵将△ABC沿AB翻折后得到△ABD,
∴△ABC≌△ABD,
∴∠ADB=∠C=90°,
∴点D在以AB为直径的⊙O上;
(2)∵△ABC≌△ABD,
∴AC=AD,
∵AB2=ACAE,
∴AB2=ADAE,即![]() ,
,
∵∠BAD=∠EAB,
∴△ABD∽△AEB,
∴∠ABE=∠ADB=90°,
∵AB为⊙O的直径,
∴BE是⊙O的切线;
(3)∵AD=AC=4、BD=BC=2,∠ADB=90°,
∴AB=![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:DE=1,
∴BE=![]() ,
,
∵四边形ACBD内接于⊙O,
∴∠FBD=∠FAC,即∠FBE+∠DBE=∠BAE+∠BAC,
又∵∠DBE+∠ABD=∠BAE+∠ABD=90°,
∴∠DBE=∠BAE,
∴∠FBE=∠BAC,
又∠BAC=∠BAD,
∴∠FBE=∠BAD,
∴△FBE∽△FAB,
∴![]() ,即
,即![]() ,
,
∴FB=2FE,
在Rt△ACF中,∵AF2=AC2+CF2,
∴(5+EF)2=42+(2+2EF)2,
整理,得:3EF2-2EF-5=0,
解得:EF=-1(舍)或EF=![]() ,
,
∴EF=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
![]() 求出每天的销售利润
求出每天的销售利润![]() 元
元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
![]() 如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?
如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?![]() 每天的总成本
每天的总成本![]() 每件的成本
每件的成本![]() 每天的销售量
每天的销售量![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
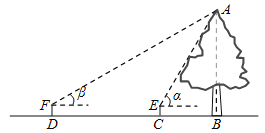
【题目】如图,AB是一棵古树,某校初四(1)班数学兴趣小组的同学想利用所学知识测出这棵古树的高,过程如下:在古树同侧的水平地面上,分别选取了C、D两点(C、D两点与古树在同一直线上),用测角仪在C处测得古树顶端A的仰角α=60°,在D处测得古树顶端A的仰角β=30°,又测得C、D两点相距14米.已知测角仪高为1.5米,请你根据他们所测得的数据求出古树AB的高.(精确到0.1米,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,点![]() 都在格点上。
都在格点上。
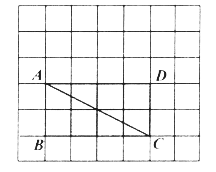
(Ⅰ)AC的长是_____________;
(Ⅱ)将四边形![]() 折叠,使点C与点4重合,折痕EF交BC于点E,交AD于点F,点D的对应点为Q,得五边形
折叠,使点C与点4重合,折痕EF交BC于点E,交AD于点F,点D的对应点为Q,得五边形![]() .请用无刻度的直尺在网格中画出折叠后的五边形,并简要说明点
.请用无刻度的直尺在网格中画出折叠后的五边形,并简要说明点![]() 的位置是如何找到的____________________.
的位置是如何找到的____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将线段 AB 先向右平移 5 个单位,再将所得线段绕原点按顺时针方向旋转 90°,得到线段 AB ,则点 B 的对应点 B′的坐标是( )

A.(-4 , 1)B.( -1, 2)C.(4 ,- 1)D.(1 ,- 2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别写着数字![]() ,1,3,6的四张卡片(卡片除数字外,其它都相同)洗匀后,背面向上放在桌子上,从中先随机抽取一张卡片,记下卡片上的数字,不放回,再从中任取一张卡片,记下数字.
,1,3,6的四张卡片(卡片除数字外,其它都相同)洗匀后,背面向上放在桌子上,从中先随机抽取一张卡片,记下卡片上的数字,不放回,再从中任取一张卡片,记下数字.
(1)请用列表或画树状图法(树状图也称树形图)中的一种方法,列出所有可能出现的结果;
(2)请计算两次摸出的卡片上的数字之和大于4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是某路灯灯架示意图,其中点A表示电灯,AB和BC为灯架,l表示地面,已知AB=2m,BC=5.7m,∠ABC=110°,BC⊥l于点C,求电灯A与地面l的距离.(结果精确到0.1m.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
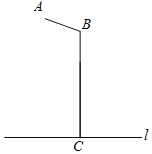
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com