
【题目】如图所示是某路灯灯架示意图,其中点A表示电灯,AB和BC为灯架,l表示地面,已知AB=2m,BC=5.7m,∠ABC=110°,BC⊥l于点C,求电灯A与地面l的距离.(结果精确到0.1m.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
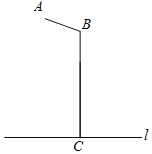
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.
1.如图1,当∠ABC=45°时,求证:AE=![]() MD;
MD;
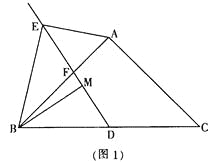
2.如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为: .
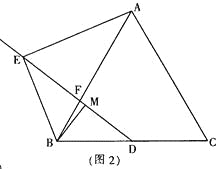
3.在(2)的条件下延长BM到P,使MP=BM,连接CP,若AB=7,AE=![]() ,求tan∠ACP的值.
,求tan∠ACP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
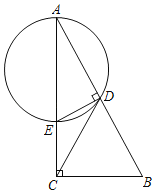
【题目】如图,在以线段AB为直径的⊙O上取一点,连接AC、BC.将△ABC沿AB翻折后得到△ABD.
(1)试说明点D在⊙O上;
(2)在线段AD的延长线上取一点E,使AB2=AC·AE.求证:BE为⊙O的切线;
(3)在(2)的条件下,分别延长线段AE、CB相交于点F,若BC=2,AC=4,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD为斜边AB的中线.过点D作AB的垂线交AC于点E,再过A、D、E三点作⊙O.
(1)确定⊙O的圆心O的位置,并证明CD为⊙O的切线;
(2)若BC=3,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△EFG中,∠EFG=90°,EF=FG,且点E,F分别在矩形ABCD的边AB,AD上.
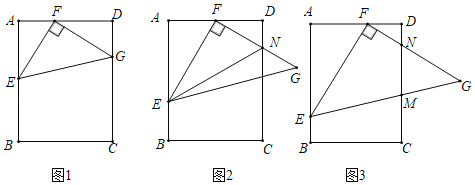
(1)如图1,当点G在CD上时,求证:△AEF≌△DFG;
(2)如图2,若F是AD的中点,FG与CD相交于点N,连接EN,求证:EN=AE+DN;
(3)如图3,若AE=AD,EG,FG分别交CD于点M,N,求证:MG2=MNMD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是由五个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后如图②.则三视图发生改变的是( )
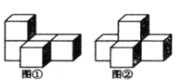
A.主视图B.俯视图
C.左视图D.主视图、俯视图和左视图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学有一块长为![]() 米,宽为
米,宽为![]() 米的矩形场地,计划在该场地上修筑宽都为2米的两条互相垂直的道路(阴影部分),余下的四块矩形小场地建成草坪.
米的矩形场地,计划在该场地上修筑宽都为2米的两条互相垂直的道路(阴影部分),余下的四块矩形小场地建成草坪.
(1)请分别写出每条道路的面积(用含![]() 或
或![]() 的代数式表示);
的代数式表示);
(2)若![]() ,并且四块草坪的面积之和为144平方米,试求原来矩形场地的长与宽各为多少米?
,并且四块草坪的面积之和为144平方米,试求原来矩形场地的长与宽各为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】祥云桥位于省城太原南部,该桥塔主体由三根曲线塔柱组合而成,全桥共设13对直线型斜拉索,造型新颖,是“三晋大地”的一种象征.某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表.
项目 | 内容 | ||
课题 | 测量斜拉索顶端到桥面的距离 | ||
测量示意图 |
| 说明:两侧最长斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内. | |
测量数据 | ∠A的度数 | ∠B的度数 | AB的长度 |
38° | 28° | 234米 | |
… | … | ||
(1)请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离(参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5)
(2)该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com