
【题目】祥云桥位于省城太原南部,该桥塔主体由三根曲线塔柱组合而成,全桥共设13对直线型斜拉索,造型新颖,是“三晋大地”的一种象征.某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表.
项目 | 内容 | ||
课题 | 测量斜拉索顶端到桥面的距离 | ||
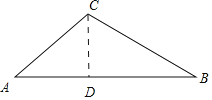
测量示意图 |
| 说明:两侧最长斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内. | |
测量数据 | ∠A的度数 | ∠B的度数 | AB的长度 |
38° | 28° | 234米 | |
… | … | ||
(1)请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离(参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5)
(2)该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可).

【答案】(1)斜拉索顶端点C到AB的距离为72米;(2)还需要补充的项目可为:测量工具,计算过程,人员分工,指导教师,活动感受等.(答案不唯一)
【解析】
(1)过点C作CD⊥AB于点D.解直角三角形求出DC即可;
(2)还需要补充的项目可为:测量工具,计算过程,人员分工,指导教师,活动感受等
(1)过点C作CD⊥AB于点D.
设CD=x米,在Rt△ADC中,∠ADC=90°,∠A=38°.
∵tan38°=![]() ,
,
∴AD=![]() .
.
在Rt△BDC中,∠BDC=90°,∠B=28°.
∵tan28°=![]() ,
,
∴BD=![]() .
.
∵AD+BD=AB=234,
∴![]() x+2x=234.
x+2x=234.
解得x=72.
答:斜拉索顶端点C到AB的距离为72米.
(2)还需要补充的项目可为:测量工具,计算过程,人员分工,指导教师,活动感受等.(答案不唯一)


科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AB//DC,AB=DC,且AB=6cm,BC=8cm,对角线AC =10cm,
(1)求证:四边形ABCD是矩形;
(2)如图(2),若动点Q从点C出发,在CA边上以每秒5cm的速度向点A匀速运动,同时动点P从点B出发,在BC边上以每秒4cm的速度向点C匀速运动,运动时间为t秒(0≤t<2),连接BQ、AP,若AP⊥BQ,求t的值;
(3)如图(3),若点Q在对角线AC上,CQ=4cm,动点P从B点出发,以每秒1cm的速度沿BC运动至点C止.设点P运动了t秒,请你探索:从运动开始,经过多少时间,以点Q、P、C为顶点的三角形是等腰三角形?请求出所有可能的结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外阅读是提高学生素养的重要途径,某校为了了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间(t小时),根据t的长短分为A,B,C,D四类.下面是根据所抽查的人数绘制的两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:

(1)求表格中的a值,并在图中补全条形统计图;
(2)该校现有1300名学生,请你估计该校共有多少学生课外阅读时间不少于1小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局今年体育测试中,从某校毕业班中抽取男,女学生各15人进行三项体育成绩复查测试.在这个问题中,下列叙述正确的是( )
A.该校所有毕业班学生是总体B.所抽取的30名学生是样本
C.样本的容量是15D.个体指的是毕业班每一个学生的体育测试成绩
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=k1x+b(k1≠0)的图象分别与x轴,y轴相交于点A,B,与反比例函数y2=![]() 的图象相交于点C(﹣4,﹣2),D(2,4).
的图象相交于点C(﹣4,﹣2),D(2,4).
(1)求一次函数和反比例函数的表达式;
(2)当x为何值时,y1>0;
(3)当x为何值时,y1<y2,请直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宜宾某商店决定购进A.B两种纪念品.购进A种纪念品7件,B种纪念品2件和购进A种纪念品5件,B种纪念品6件均需80元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于750元,但不超过764元,那么该商店共有几种进货方案?
(3)已知商家出售一件A种纪念品可获利a元,出售一件B种纪念品可获利(5﹣a)元,试问在(2)的条件下,商家采用哪种方案可获利最多?(商家出售的纪念品均不低于成本价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°,
证明:过点C作CF∥AB.
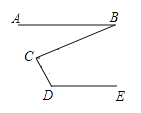
∵AB∥CF(已知),
∴∠B= ( ).
∵AB∥DE,CF∥AB( 已知 ),
∴CF∥DE ( )
∴∠2+ =180° ( )
∵∠2=∠BCD﹣∠1,
∴∠D+∠BCD﹣∠B=180° ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() -1来表示
-1来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:∵![]() ,即
,即![]() ,
,
∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() -2).
-2).
请解答:(1) ![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a, ![]() 的整数部分为b,求a+b-
的整数部分为b,求a+b-![]() 的值;
的值;
(3)已知: 10+![]() =x+y,其中x是整数,且0<y<1,求x-y的相反数.
=x+y,其中x是整数,且0<y<1,求x-y的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AD⊥BC于点D,CE⊥AB于点E.

(1)猜测∠1与∠2的关系,并说明理由;
(2)如果∠ABC是钝角,如图2,(1)中的结论是否还成立?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com