
ЁОЬтФПЁПвЫБіФГЩЬЕъОіЖЈЙКНјAЃЎBСНжжМЭФюЦЗЃЎЙКНјAжжМЭФюЦЗ7МўЃЌBжжМЭФюЦЗ2МўКЭЙКНјAжжМЭФюЦЗ5МўЃЌBжжМЭФюЦЗ6МўОљаш80дЊЃЎ
ЃЈ1ЃЉЧѓЙКНјAЁЂBСНжжМЭФюЦЗУПМўИїашЖрЩйдЊЃП
ЃЈ2ЃЉШєИУЩЬЕъОіЖЈЙКНјетСНжжМЭФюЦЗЙВ100МўЃЌПМТЧЪаГЁашЧѓКЭзЪН№жмзЊЃЌгУгкЙКТђет100МўМЭФюЦЗЕФзЪН№ВЛЩйгк750дЊЃЌЕЋВЛГЌЙ§764дЊЃЌФЧУДИУЩЬЕъЙВгаМИжжНјЛѕЗНАИЃП
ЃЈ3ЃЉвбжЊЩЬМвГіЪлвЛМўAжжМЭФюЦЗПЩЛёРћaдЊЃЌГіЪлвЛМўBжжМЭФюЦЗПЩЛёРћЃЈ5ЉaЃЉдЊЃЌЪдЮЪдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЩЬМвВЩгУФФжжЗНАИПЩЛёРћзюЖрЃПЃЈЩЬМвГіЪлЕФМЭФюЦЗОљВЛЕЭгкГЩБОМлЃЉ
ЁОД№АИЁПЃЈ1ЃЉAжжМЭФюЦЗУПМўаш10дЊЁЂBжжМЭФюЦЗУПМўаш5дЊЃЛЃЈ2ЃЉгаШ§жжЗНАИЃЛЃЈ3ЃЉЕБaЃН2.5ЪБЃЌШ§жжЗНАИЛёРћЯрЭЌЃЛЕБ0ЁмaЃМ2.5ЪБЃЌЗНАИвЛЛёРћзюЖрЃЛЕБ2.5ЃМaЁм5ЪБЃЌЗНАИШ§ЛёРћзюЖр
ЁОНтЮіЁП
ЃЈ1ЃЉЩшЙКНјAжжМЭФюЦЗУПМўашxдЊЁЂBжжМЭФюЦЗУПМўашyдЊЃЌИљОнЬтвтЕУЙигкxКЭyЕФЖўдЊвЛДЮЗНГЬзщЃЌНтЕУxКЭyЕФжЕМДПЩЃЛ
ЃЈ2ЃЉЩшЙКНјAжжМЭФюЦЗtМўЃЌдђЙКНјBжжМЭФюЦЗЃЈ100ЉtЃЉМўЃЌгЩЬтвтЕУЙигкtЕФВЛЕШЪНЃЌНтЕУtЕФЗЖЮЇЃЌдйгЩtЮЊе§ећЪ§ЃЌПЩЕУtЕФжЕЃЌДгЖјЗНАИЪ§ПЩЕУЃЛ
ЃЈ3ЃЉЗжБ№аДГіШ§жжЗНАИЙигкaЕФРћШѓКЏЪ§ЃЌИљОнвЛДЮКЏЪ§ЕФаджЪПЩЕУД№АИЃЎ
НтЃКЃЈ1ЃЉЩшЙКНјAжжМЭФюЦЗУПМўашxдЊЁЂBжжМЭФюЦЗУПМўашyдЊЃЌ
ИљОнЬтвтЕУЃК![]()
НтЕУЃК![]()
Д№ЃКЙКНјAжжМЭФюЦЗУПМўаш10дЊЁЂBжжМЭФюЦЗУПМўаш5дЊЃЛ
ЃЈ2ЃЉЩшЙКНјAжжМЭФюЦЗtМўЃЌдђЙКНјBжжМЭФюЦЗЃЈ100ЉtЃЉМўЃЌ
гЩЬтвтЕУЃК750Ём5t+500Ём764
НтЕУ![]()
ЁпtЮЊе§ећЪ§
ЁрtЃН50ЃЌ51ЃЌ52
ЁргаШ§жжЗНАИЃЎ
ЕквЛжжЗНАИЃКЙКНјAжжМЭФюЦЗ50МўЃЌBжжМЭФюЦЗ50МўЃЛ
ЕкЖўжжЗНАИЃКЙКНјAжжМЭФюЦЗ51МўЃЌBжжМЭФюЦЗ50МўЃЛ
ЕкШ§жжЗНАИЃКЙКНјAжжМЭФюЦЗ52МўЃЌBжжМЭФюЦЗ48МўЃЛ
ЃЈ3ЃЉЕквЛжжЗНАИЩЬМвПЩЛёРћЃКwЃН50a+50ЃЈ5ЉaЃЉЃН250ЃЈдЊЃЉЃЛ
ЕкЖўжжЗНАИЩЬМвПЩЛёРћЃКwЃН51a+49ЃЈ5ЉaЃЉЃН245+2aЃЈдЊЃЉЃЛ
ЕкШ§жжЗНАИЩЬМвПЩЛёРћЃКwЃН52a+48ЃЈ5ЉaЃЉЃН240+4aЃЈдЊЃЉЃЎ
ЕБaЃН2.5ЪБЃЌШ§жжЗНАИЛёРћЯрЭЌЃЛ
ЕБ0ЁмaЃМ2.5ЪБЃЌЗНАИвЛЛёРћзюЖрЃЛ
ЕБ2.5ЃМaЁм5ЪБЃЌЗНАИШ§ЛёРћзюЖрЃЎ


 ЧсЫЩЪюМйзмИДЯАЯЕСаД№АИ
ЧсЫЩЪюМйзмИДЯАЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуAЁЂBЪЧЪ§жсЩЯЕФСНИіЕуЃЌЫќУЧЗжБ№БэЪОЕФЪ§ЪЧ![]() КЭ1ЃЎ ЕуAгыЕуBжЎМфЕФОрРыБэЪОЮЊABЃЎ
КЭ1ЃЎ ЕуAгыЕуBжЎМфЕФОрРыБэЪОЮЊABЃЎ
ЃЈ1ЃЉAB= ЃЎ
ЃЈ2ЃЉЕуPЪЧЪ§жсЩЯAЕугвВрЕФвЛИіЖЏЕуЃЌЫќБэЪОЕФЪ§ЪЧ![]() ЃЌТњзу
ЃЌТњзу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ3ЃЉЕуCЮЊ6ЃЎ ШєЕуAвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЭЌЪБЃЌЕуBКЭЕуCЗжБ№вдУПУы2ИіЕЅЮЛГЄЖШКЭ5ИіЕЅЮЛГЄЖШЕФЫйЖШЯђгвдЫЖЏЃЎЧыЮЪЃК![]() ЕФжЕЪЧЗёЫцзХдЫЖЏЪБМфtЃЈУыЃЉЕФБфЛЏЖјИФБфЃП ШєБфЛЏЃЌЧыЫЕУїРэгЩЃЛШєВЛБфЃЌЧыЧѓЦфжЕЃЎ
ЕФжЕЪЧЗёЫцзХдЫЖЏЪБМфtЃЈУыЃЉЕФБфЛЏЖјИФБфЃП ШєБфЛЏЃЌЧыЫЕУїРэгЩЃЛШєВЛБфЃЌЧыЧѓЦфжЕЃЎ
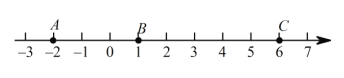
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкГЄЗНаЮ ![]() жаЃЌ
жаЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЕу
ЃЌЕу ![]() ДгЕу
ДгЕу ![]() ГіЗЂЃЌвд
ГіЗЂЃЌвд ![]() ЕФЫйЖШби
ЕФЫйЖШби ![]() ЯђЕу
ЯђЕу ![]() дЫЖЏЃЌЩшЕу
дЫЖЏЃЌЩшЕу ![]() ЕФдЫЖЏЪБМфЮЊ
ЕФдЫЖЏЪБМфЮЊ ![]() УыЃК
УыЃК 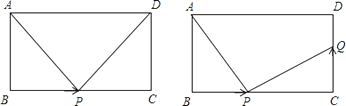
ЃЈ1ЃЉ![]()
![]() .(гУ
.(гУ ![]() ЕФДњЪ§ЪНБэЪО)
ЕФДњЪ§ЪНБэЪО)
ЃЈ2ЃЉ ЕБ ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ ![]()
ЃЈ3ЃЉЕБЕу ![]() ДгЕу
ДгЕу ![]() ПЊЪМдЫЖЏЃЌЭЌЪБЃЌЕу
ПЊЪМдЫЖЏЃЌЭЌЪБЃЌЕу ![]() ДгЕу
ДгЕу ![]() ГіЗЂЃЌвд v
ГіЗЂЃЌвд v![]() ЕФЫйЖШби
ЕФЫйЖШби ![]() ЯђЕу
ЯђЕу ![]() дЫЖЏЃЌЪЧЗёДцдкетбљЕФv жЕЃЌЪЙЕУ
дЫЖЏЃЌЪЧЗёДцдкетбљЕФv жЕЃЌЪЙЕУ ![]() ШЋЕШЃПШєДцдкЃЌЧыЧѓГі vЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ШЋЕШЃПШєДцдкЃЌЧыЧѓГі vЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭМaЪЧвЛИіГЄЮЊ2 mЁЂПэЮЊ2 nЕФГЄЗНаЮ, биЭМжаащЯпгУМєЕЖОљЗжГЩЫФПщаЁГЄЗНаЮ, ШЛКѓАДЭМbЕФаЮзДЦДГЩвЛИіе§ЗНаЮЁЃ
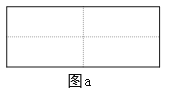

(1)ФуШЯЮЊЭМbжаЕФвѕгАВПЗжЕФе§ЗНаЮЕФБпГЄЕШгк__________________ЁЃ
(2)ЧыгУСНжжВЛЭЌЕФЗНЗЈЧѓЭМbжавѕгАВПЗжЕФУцЛ§ЁЃ
ЗНЗЈ1ЃК___________________________ ЗНЗЈ2ЃК___________________________
(3)ЙлВьЭМbЃЌФуФмаДГіЯТСаШ§ИіДњЪ§ЪНжЎМфЕФЕШСПЙиЯЕТ№?
ДњЪ§ЪН: ЃЈm+nЃЉ2 ЃЌЃЈm-nЃЉ2ЃЌmn
_______________________________________________________
(4)ИљОнЃЈ3ЃЉЬтжаЕФЕШСПЙиЯЕЃЌНтОіШчЯТЮЪЬтЃК
Шєa+b=7ЃЌab=5ЃЌЧѓЃЈa-bЃЉ2ЕФжЕЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ2ЕФЕШБпЁїABCжаЃЌDЪЧBCЕФжаЕуЃЌЕуEдкЯпЖЮADЩЯЃЌСЌНсBEЃЌдкBEЕФЯТЗНзїЕШБпЁїBEFЃЌСЌНсDFЃЎЕБЁїBDFЕФжмГЄзюаЁЪБЃЌЁЯDBFЕФЖШЪ§ЪЧ_____ЃЎ
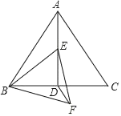
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛДќзгжазАгааЮзДДѓаЁЖМЯрЭЌЕФЫФИіаЁЧђЃЌУПИіаЁЧђЩЯИїБъгавЛИіЪ§зжЃЌЗжБ№ЪЧ1,4,7,8.ЯжЙцЖЈДгДќзгжаШЮШЁвЛИіаЁЧђЃЌЖдгІЕФЪ§зжзїЮЊвЛИіСНЮЛЪ§ЕФЪЎЮЛЪ§ЃЛШЛКѓНЋаЁЧђЗХЛиДќзгжаВЂНСАшОљдШЃЌдйШЮШЁвЛИіаЁЧђЃЌЖдгІЪ§зжзїЮЊетИіСНЮЛЪ§ЕФЕФИіЮЛЪ§.
ЃЈ1ЃЉгУЪїзДЭМЛђСаБэЕФЗНЗЈЃЌаДГіАДееЩЯЪіЙцЖЈЕУЕНЫљгаПЩФмЕФСНЮЛЪ§ЃЛ
ЃЈ2ЃЉДгетаЉСНЮЛЪ§жаШЮШЁвЛИіЃЌЧѓЦфЫуЪѕЦНЗНИљДѓгк4ЧваЁгк7ЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦНУцжБНЧзјБъЯЕ ![]() жаЃЌ
жаЃЌ ![]() ЪЧзјБъдЕуЁЃвбжЊA(0,
ЪЧзјБъдЕуЁЃвбжЊA(0, ![]() )ЃЌB(1,0)ЃЌCЃЈ6,
)ЃЌB(1,0)ЃЌCЃЈ6, ![]() ЃЉЃЌгавЛХзЮяЯпЧЁКУОЙ§етШ§Еу.
ЃЉЃЌгавЛХзЮяЯпЧЁКУОЙ§етШ§Еу.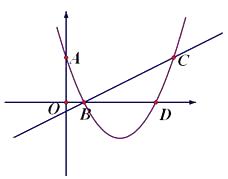
ЃЈ1ЃЉЧѓИУХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉШєХзЮяЯпНЛ ![]() жсЕФСэвЛНЛЕуЮЊDЃЌФЧУДХзЮяЯпЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЕУ
жсЕФСэвЛНЛЕуЮЊDЃЌФЧУДХзЮяЯпЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЕУ ![]() ,ШєДцдкЃЌЧѓГіPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
,ШєДцдкЃЌЧѓГіPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКХзЮяЯп ![]() ОЙ§зјБъдЕуЃЌЧвЕБ
ОЙ§зјБъдЕуЃЌЧвЕБ ![]() ЪБ, yЫцxЕФдіДѓЖјМѕаЁ.
ЪБ, yЫцxЕФдіДѓЖјМѕаЁ.
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЯТЭМЃЌЩшЕуAЪЧИУХзЮяЯпЩЯЮЛгкxжсЯТЗНЕФвЛИіЖЏЕуЃЌЙ§ЕуAзїxжсЕФЦНааЯпНЛХзЮяЯпгкСэвЛЕуDЃЌдйзїAB ![]() xжсгкЕуB, DC
xжсгкЕуB, DC ![]() xжсгкЕуC.
xжсгкЕуC.
ЂйЕБ BC=1ЪБЃЌжБНгаДГіОиаЮABCDЕФжмГЄЃЛ
ЂкЩшЖЏЕуAЕФзјБъЮЊЃЈa, bЃЉ,НЋОиаЮABCDЕФжмГЄLБэЪОЮЊaЕФКЏЪ§ЃЌВЂаДГіздБфСПЕФШЁжЕЗЖЮЇЃЌХаЖЯжмГЄЪЧЗёДцдкзюДѓжЕЃЌШчЙћДцдкЃЌЧѓГіетИізюДѓжЕЃЌВЂЧѓГіДЫЪБЕуAЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§yЃНax2ЃЋbxЃЋc(aЁй0)ЕФЭМЯѓШчЭМЃЌЖдГЦжсЪЧжБЯпxЃН1ЃЌгавдЯТЫФИіНсТлЃК
ЂйabcЃО0ЃЛЂкb2Ѓ4acЃО0ЃЛЂлbЃНЃ2aЃЛЂмaЃЋbЃЋcЃО2ЃЎЦфжае§ШЗЕФЪЧ (ЬюаДађКХ)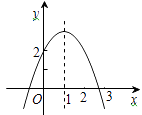
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com