
【题目】已知:在△ABC中AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.
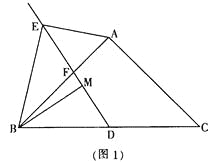
1.如图1,当∠ABC=45°时,求证:AE=![]() MD;
MD;
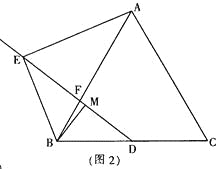
2.如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为: .
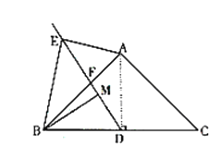
3.在(2)的条件下延长BM到P,使MP=BM,连接CP,若AB=7,AE=![]() ,求tan∠ACP的值.
,求tan∠ACP的值.
【答案】(1)证明见解析;(2)AE=2MD;(3)tan∠ACP= ![]() .
.
【解析】
(1)由题意知∠BAE=∠BDM,∠ABE=∠DBM故有△ABE∽△DBMAE:DM=AB:BD,而∠ABC=45°AB=![]() BD,则有AE=
BD,则有AE=![]() MD;
MD;
(2)由于△ABE∽△DBM,相似比为2,进而确定出AE与DM的关系;
(3)由题意知得△BEP为等边三角形,有EM⊥BP,∠BMD=∠AEB=90°,在Rt△AEB中求得AE、AB、tan∠EAB的值,由D为BC中点,M为BP中点,得DM∥PC,求得tan∠PCB的值,在Rt△ABD和Rt△NDC中,由锐角三角函数的定义求得AD、ND的值,进而求得tan∠ACP的值.
(1)证明:如图1 连接AD
∵AB=AC,BD=CD,
∴AD⊥BC,
又∵∠ABC=45°,
∴BD=ABcos∠ABC,即AB=![]() BD.
BD.
∵∠BAE=∠BDM,∠ABE=∠DBM,
∴△ABE∽△DBM
∴![]() ,
,
∴AE=![]() MD.
MD.
(2)AE=2MD
如图2,连接AD,EP,过N作NH⊥AC,垂足为H,连接NH,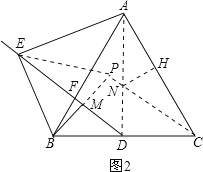
∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
又∵D为BC的中点,
∴AD⊥BC,∠DAC=30°,BD=DC=![]() AB,
AB,
∵∠BAE=∠BDM,∠ABE=∠DBM,
∴△ABE∽△DBM,
∴![]() ,即AE=2DM;
,即AE=2DM;
(3)解:如图2 由(2)得△ABE∽△DBM,
∴![]() ,∠AEB=∠DMB,
,∠AEB=∠DMB,
∴EB=2BM,
又∵BM=MP
∴EB=BP,
又∵∠EBM=∠ABC=60°,
∴△BEP为等边三角形,
∴EM⊥BP,
∴∠BMD=90° ,
∴∠AEB=90°,
在Rt△AEB中,AE=2![]() ,AB=7,
,AB=7,
∴![]() =
=![]() ,
,
∵D为BC中点 M为PB中点,
∴DM//PC,
∴∠MDB=∠PCB,
∴∠EAB=∠PCB,
∴tan∠PCB=![]() ,
,
在RT△ABD中,AD=ABsin∠ABD=![]() ,
,
在RT△NDC中,ND=CDtan∠NCD ==![]() ,
,
∴NA=AD-ND=![]() ,
,
过N作NH⊥AC,垂足为H,
在RT△ANH中,NH=![]() AH=
AH=![]() ,AH=ANcos∠NAH=
,AH=ANcos∠NAH=![]() ,
,
∴CH=AC-AH=![]() ,
,
∴tan∠ACP=![]() =
=![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
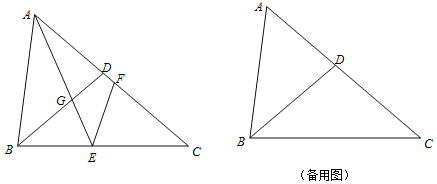
【题目】如图,已知△ABC中,AB=8,BC=10,AC=12,D是AC边上一点,且AB2=ADAC,连接BD,点E、F分别是BC、AC上两点(点E不与B、C重合),∠AEF=∠C,AE与BD相交于点G.
(1)求BD的长;
(2)求证△BGE∽△CEF;
(3)连接FG,当△GEF是等腰三角形时,直接写出BE的所有可能的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.
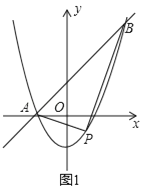

(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
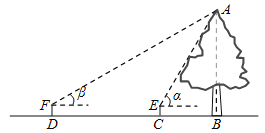
【题目】如图,AB是一棵古树,某校初四(1)班数学兴趣小组的同学想利用所学知识测出这棵古树的高,过程如下:在古树同侧的水平地面上,分别选取了C、D两点(C、D两点与古树在同一直线上),用测角仪在C处测得古树顶端A的仰角α=60°,在D处测得古树顶端A的仰角β=30°,又测得C、D两点相距14米.已知测角仪高为1.5米,请你根据他们所测得的数据求出古树AB的高.(精确到0.1米,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
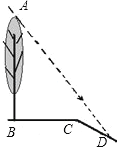
【题目】如图,坡面CD的坡比为![]() ,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC=3米,斜坡上的树影CD=
,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC=3米,斜坡上的树影CD=![]() 米,则小树AB的高是 .
米,则小树AB的高是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,点![]() 都在格点上。
都在格点上。
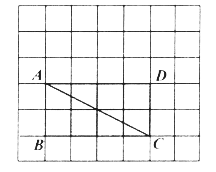
(Ⅰ)AC的长是_____________;
(Ⅱ)将四边形![]() 折叠,使点C与点4重合,折痕EF交BC于点E,交AD于点F,点D的对应点为Q,得五边形
折叠,使点C与点4重合,折痕EF交BC于点E,交AD于点F,点D的对应点为Q,得五边形![]() .请用无刻度的直尺在网格中画出折叠后的五边形,并简要说明点
.请用无刻度的直尺在网格中画出折叠后的五边形,并简要说明点![]() 的位置是如何找到的____________________.
的位置是如何找到的____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将线段 AB 先向右平移 5 个单位,再将所得线段绕原点按顺时针方向旋转 90°,得到线段 AB ,则点 B 的对应点 B′的坐标是( )

A.(-4 , 1)B.( -1, 2)C.(4 ,- 1)D.(1 ,- 2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是某路灯灯架示意图,其中点A表示电灯,AB和BC为灯架,l表示地面,已知AB=2m,BC=5.7m,∠ABC=110°,BC⊥l于点C,求电灯A与地面l的距离.(结果精确到0.1m.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
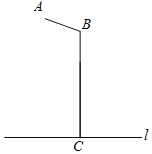
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
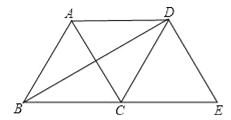
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com