
【题目】平面内,如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 为
为![]() 边上任意一点,连接
边上任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() .
.
(1)当![]() 时,求
时,求![]() 的大小;
的大小;
(2)当![]() 时,求点
时,求点![]() 与点
与点![]() 间的距离(结果保留根号);
间的距离(结果保留根号);
(3)若点![]() 恰好落在
恰好落在![]() 的边所在的直线上,直接写出
的边所在的直线上,直接写出![]() 旋转到
旋转到![]() 所扫过的面积(结果保留
所扫过的面积(结果保留![]() ).
).
【答案】(1)100°或80°;(2)![]() ;(3)16π或20π或32π.
;(3)16π或20π或32π.
【解析】
试题分析:(1)根据点Q与点B和PD的位置关系分类讨论;(2)因为△PBQ是等腰直角三角形,所以求BQ的长,只需求PB,过点P作PH⊥AB于点H,确定AH:BH,求得AH和BH,解直角△APH求PH,由勾股定理求PB.(3)根据点Q在AD上,DC上,BC的延长线上,分别画出图形,分三种情况讨论.
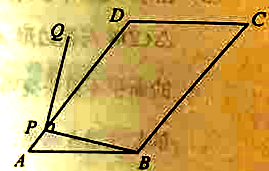
试题解析:(1)当点Q与B在PD的异侧时,由∠DPQ=10°,∠BPQ=90°得∠BPD=80°,
∴∠APB=180°-∠BPD=100°.
当点Q与B在PD的同侧时,如图2,∠APB=180°-∠BPQ-∠DPQ=80°.
∴∠APB的度数是80°或100°.
(2)如图2,过点P作PH⊥AB于点H,连接BQ.
∵tan∠ABP:tanA=![]() ,∴AH:HB=3:2.
,∴AH:HB=3:2.
而AB=10,∴AH=6,HB=4.
在Rt△PHA中,PH=AH·tanA=8.
∴PQ=PB=![]() .
.
∴在Rt△PQB中,QB=![]() PB=
PB=![]() .
.

(3)①点Q在AD上时,如图3,由tanA=![]() 得,PB=AB·sinA=8,∴扇形面积为16π.
得,PB=AB·sinA=8,∴扇形面积为16π.



②点A在CD上时,如图4,过点P作PH⊥AB于点H,交CD延长线于点K,由题意∠K=90°,∠KDP=∠A.
设AH=x,则PH=AH·tanA=![]() .
.
∵∠BPH=∠KQP=90°-∠KPQ,PB=QP,∴Rt△HPB≌Rt△KQP.∴KP=HB=10-x.
∴AP=![]() ,PD=
,PD=![]() ,AD=15=
,AD=15=![]() ,解得x=6.
,解得x=6.
∵![]() ,∴扇形的面积为20π.
,∴扇形的面积为20π.
③点Q在BC延长线上时,如图5,过点B作BM⊥AD于点M,由①得BM=8.
又∠MPB=∠PBQ=45°,∴PB=![]() ,∴扇形面积为32π.
,∴扇形面积为32π.
所以扇形的面积为16π或20π或32π.


科目:初中数学 来源: 题型:
【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.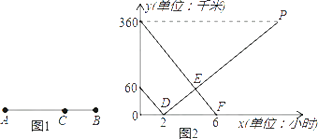
(1)填空:A , B两地相距千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)客、货两车何时相遇?相遇处离C站的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《“一带一路”贸易合作大数据报告(2017)》以“一带一路”贸易合作现状分析和趋势预测为核心,采集调用了8000多个种类,总计1.2亿条全球进出口贸易基础数据…,1.2亿用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀的传统文化,市教育局决定开展“经典诵读进校园”活动,某校园团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表:
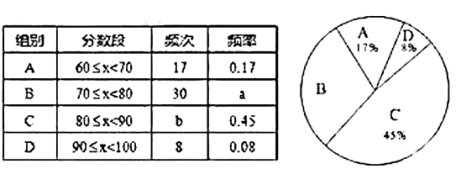
请根据所给信息,解答以下问题:
(1)表中![]() ;
;![]() ;
;
(2)请计算扇形统计图中![]() 组对应的圆心角的度数;
组对应的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列举法或树状图法求甲、乙两名同学都被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具店用2000元购进一批玩具,面市后,供不应求,于是店主又购进同样的玩具,所购的数量是第一批数量的3倍,但进价贵了4元,结果购进第二批玩具共用了6300元,若两批玩具的售价都是120元,且两批玩具全部售完,求该玩具店销售这两批玩具共盈利多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com