
【题目】已知△ABC的三边长分别为a,b,c.
(1)若a,b,c满足a2+b2+c2=ab+bc+ca,试判断△ABC的形状;
(2)若a=5,b=2,且c为整数,求△ABC的周长的最大值及最小值.
【答案】(1)等边三角形;(2)最大值为13;最小值为11
【解析】
(1)根据等式的性质将等式变形为2a2+2b2+2c2=2ab+2bc+2ca,然后再利用完全平方公式进行变形,然后直接根据非负数的性质即可得出结论;
(2)根据三角形的三边关系可得出c的取值范围,进而可得出结论.
解:由题意可知2a2+2b2+2c2=2ab+2bc+2ca
∴2a2+2b2+2c2-2ab-2bc-2ca=0
![]()
![]()
又∵![]()
∴![]()
∴![]() ,即a=b=c
,即a=b=c
∴△ABC为等边三角形
(2)∵a=5,b=2,且c为整数,
∴5-2<c<5+2,即3<c<7,
∴c=4,5,6,
∴当c=4时,△ABC周长的最小值=5+2+4=11;
当c=6时,△ABC周长的最大值=5+2+6=13.


科目:初中数学 来源: 题型:
【题目】已知方程:x![]() ﹣2x﹣8=0,解决一下问题:
﹣2x﹣8=0,解决一下问题:
(1)不解方程判断此方程的根的情况;
(2)请按要求分别解这个方程:①配方法;②因式分解法.
(3)这些方法都是将解 转化为解 ;
(4)尝试解方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话。
⑴现有1,2,3,4,5,6,7,8,9共九个数字,请将它们分别填入图1的九个方格中,使得每行的三个数、每列的三个数、斜对角的三个数之和都等于15.
⑵通过研究问题⑴,利用你发现的规律,将3,5,-7,1,7,-3,9,-5,-1
这九个数字分别填入图2的九个方格中,使得横、竖、斜对角的所有三个数的和都相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用![]() 元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高
元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高![]() 元,商店用了
元,商店用了![]() 元,所购数量是第一次的
元,所购数量是第一次的![]() 倍.
倍.
(1)求第一批采购的书包的单价是多少元?
(2)若商店按售价为每个书包![]() 元,销售完这两批书包,总共获利多少元?
元,销售完这两批书包,总共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为4000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%.
(1)设该学校所买的电脑台数是x台,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别写出
元,请分别写出![]() ,
, ![]() 与x之间的关系式;
与x之间的关系式;
(2)该学校如何根据所买电脑的台数选择到哪间商场购买,所需费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 今年6月份,我市某果农收获荔枝30吨,香蕉13吨.现计划租用甲、乙两种货车共10辆将这批水果全部运往深圳,已知甲种货车可将荔枝4吨和香蕉1吨,乙种货车可将荔枝和香蕉各2吨.
(1)该果农安排甲、乙两种货车时有几种方案?请你帮助设计出来?
(2)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输1300元,则该果农应选择哪能种方案才能使运输费最少?最少动费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
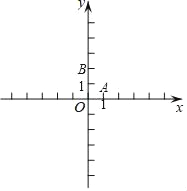
【题目】已知在平面直角坐标系xOy(如图)中,已知抛物线y=![]() +bx+c点经过A(1,0)、B(0,2).
+bx+c点经过A(1,0)、B(0,2).
(1)求该抛物线的表达式;
(2)设该抛物线的对称轴与x轴的交点为C,第四象限内的点D在该抛物线的对称轴上,如果以点A、C、D所组成的三角形与△AOB相似,求点D的坐标;
(3)设点E在该抛物线的对称轴上,它的纵坐标是1,联结AE、BE,求sin∠ABE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com