
【题目】已知方程:x![]() ﹣2x﹣8=0,解决一下问题:
﹣2x﹣8=0,解决一下问题:
(1)不解方程判断此方程的根的情况;
(2)请按要求分别解这个方程:①配方法;②因式分解法.
(3)这些方法都是将解 转化为解 ;
(4)尝试解方程:![]() .
.
【答案】(1)此方程有两个不相等的实数根;(2)①x1=4,x2=﹣2;②x1=4,x2=﹣2;(3)一元二次方程;一元一次方程;(4)x1=0,x2=x3=﹣1.
【解析】
(1)由根的判别式△=b2-4ac=36,可判断出此方程有两个不相等的实数根;
(2)①按照配方法解方程的步骤一步步解方程;②按照分解因式法解方程的步骤一步步解方程;
(3)解方程的方法都是达到降次的目的,故可出结论;
(4)利用分解因式解方程的方法一步步解决方程.
(1)∵a=1,b=﹣2,c=﹣8,
∴△=b2﹣4ac=(﹣2)2﹣4×1×(﹣8)=36>0,
∴此方程有两个不相等的实数根;
(2)①配方法:∵x2﹣2x﹣8=0,
∴x2﹣2x=8,
∴x2﹣2x+1=8+1,
∴(x﹣1)2=9,
∴x﹣1=±3, 解得:x1=4,x2=﹣2;
②因式分解法:∵x2﹣2x﹣8=0,
∴(x﹣4)(x+2)=0, 解得:x1=4,x2=﹣2;
(3)答案为:一元二次方程;一元一次方程;
(4)∵x3+2x2+x=0,
∴x(x2+2x+1)=0,
∴x(x+1)2=0,
∴x=0,x+1=0, 解得:x1=0,x2=x3=﹣1.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数y=![]() (k≠0)的图象过点C,则该反比例函数的表达式为_______.
(k≠0)的图象过点C,则该反比例函数的表达式为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
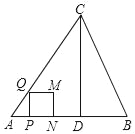
【题目】如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
(1)直接写出tanB的值为 .
(2)求点M落在边BC上时t的值.
(3)当正方形PQMN与△ABC重叠部分为四边形时,求S与t之间的函数关系式.
(4)边BC将正方形PQMN的面积分为1:3两部分时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着网络的发展,我们的生活越来越方便,越来越多的人在网络上购物,微商这个行业也悄然兴起,很多人通过微信平台销售商品.
(1)某水果微商今年九月购进榴莲和奇异果共1000千克,它们的进价均为每千克24 元,然后以榴莲售价每千克45元,奇异果售价每千克36元的价格很快销售完,若该水果微商九月获利不低于17400元,求应购进榴莲至少多少千克?
(2)为了增加销售量,获得更大的利润,在进价不变的情况下,该水果微商十月决定调整售价,榴莲的售价在九月的基础上下调![]() (降价后的售价不低于进价),奇异果的售价在九月的基础上上涨
(降价后的售价不低于进价),奇异果的售价在九月的基础上上涨![]() ,同时,与(1)中获得的最低利润时的销售量相比,榴莲的销售量下降了
,同时,与(1)中获得的最低利润时的销售量相比,榴莲的销售量下降了![]() ,而奇异果的销售量上升了
,而奇异果的销售量上升了![]() ,结果十月的销售额比九月增加了600元.求
,结果十月的销售额比九月增加了600元.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D. 下列结论:①AD是∠BAC的平分线;②点D在AB的垂直平分线上;③∠ADC=60°;④![]() 。其中正确的结论有( )
。其中正确的结论有( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1: 2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三边长分别为a,b,c.
(1)若a,b,c满足a2+b2+c2=ab+bc+ca,试判断△ABC的形状;
(2)若a=5,b=2,且c为整数,求△ABC的周长的最大值及最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com