
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴的交点
轴的交点![]() 在
在![]() 和
和![]() 之间(不包括这两点),对称轴为直线
之间(不包括这两点),对称轴为直线![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的是________.
.其中正确的是________.

【答案】①③④⑤
【解析】
①由抛物线的开口方向、对称轴以及与y轴的交点,可得出a>0、b<0、c<0,进而可得出abc>0,结论①正确;②由抛物线的对称轴及点A的坐标,可得出抛物线与x轴的另一交点坐标,结合抛物线的开口可得出当x=2时,y=4a+2b+c<0,结论②错误;③由a>0、b<0、c<0,可得出![]() ,结论③正确;④由当x=-1时y=a-b+c=0,结合b=-2a可得出3a=-c,再根据-2<c<-1,即可求出
,结论③正确;④由当x=-1时y=a-b+c=0,结合b=-2a可得出3a=-c,再根据-2<c<-1,即可求出![]() ,结论④正确;⑤由a-b+c=0、a>0,可得出-b+c<0,即b>c,结论⑤正确.综上即可得出结论.
,结论④正确;⑤由a-b+c=0、a>0,可得出-b+c<0,即b>c,结论⑤正确.综上即可得出结论.
①∵抛物线开口向上,对称轴为直线x=1,与y轴的交点在(0,2)和(0,1)之间,
∴a>0, ![]() ,2<c<1,
,2<c<1,
∴b<0,abc>0,结论①正确;
②∵抛物线与x轴交于点A(1,0),对称轴为直线x=1,
∴抛物线与x轴的另一交点坐标为(3,0),
∴当x=2时,y=4a+2b+c<0,结论②错误;
③∵a>0,b<0,c<0,
∴4ac<0, ![]() >0,
>0,
∴![]() ,结论③正确;
,结论③正确;
④当x=1时,y=ab+c=0,
∴ab=c.
∵b=2a,
∴3a=c.
又∵2<c<1,
∴![]() ,结论④正确;
,结论④正确;
⑤∵当x=1时,y=ab+c=0,a>0,
∴b+c<0,
∴b>c,结论⑤正确。
综上所述:正确的结论有①③④⑤.
故答案为:①③④⑤.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:初中数学 来源: 题型:
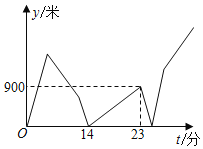
【题目】已知A、B、C三地顺次在同一直线上,甲、乙两人均骑车从A地出发,向C地匀速行驶.甲比乙早出发5分钟,甲到达B地并休息了2分钟后,乙追上了甲.甲、乙同时从B地以各自原速继续向C地行驶.当乙到达C地后,乙立即掉头并提速为原速的![]() 倍按原路返回A地,而甲也立即提速为原速的
倍按原路返回A地,而甲也立即提速为原速的![]() 倍继续向C地行驶,到达C地就停止.若甲、乙间的距离y(米)与甲出发的时间t(分)之间的函数关系如图所示,则当甲到达C地时,乙距A地_____米.
倍继续向C地行驶,到达C地就停止.若甲、乙间的距离y(米)与甲出发的时间t(分)之间的函数关系如图所示,则当甲到达C地时,乙距A地_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一根长22cm的铁丝,
(1)能否围成面积是30cm2的矩形?如果能,求出矩形的边长,如果不能说明理由;
(2)能否围成面积是32cm2的矩形?如果能,求出矩形的边长,如果不能说明理由;
(3)请探索能围成的矩形面积的最大值是多少 cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下的公式:
①cos(α+β)=cosαcosβ﹣sinαsinβ;sin(α+β)=sinαcosβ+cosαsinβ;
②tan(α+β)=![]() .
.
③利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值,如tan105°=tan(45°+60°)=![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
根据上面的知识,你可以选择适当的公式解决下面的实际问题:
(1)求cos75°的值;
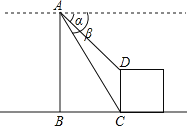
(2)如图,直升机在一建筑物CD上方的点A处测得建筑物顶端点D的俯角α为60°,底端点C的俯角β为75°,此时直升机与建筑物CD的水平距离BC为42m,求建筑物CD的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一道满分12分的解答题,按评分标准,所有考生的得分只有四种:0分,4分,8分,12分.老师为了了解学生的得分情况与题目的难易情况,从所有考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
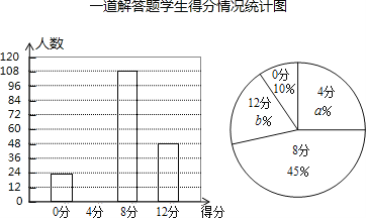
请根据以上信息解答下列问题:
(1)填空:a=______,b=______,并把条形统计图补全;
(2)已知难度系数的计算公式为![]() ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0≤L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L≤1时,此题为容易题.试问此题对于这些考生来说属于哪一类?请说明理由.
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0≤L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L≤1时,此题为容易题.试问此题对于这些考生来说属于哪一类?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数经过点B(3,0),C(0,3),D(4,-5)
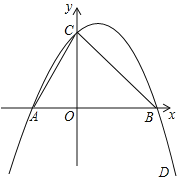
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)若P是抛物线上一点,且S△ABP=![]() S△ABC,这样的点P有几个请直接写出它们的坐标.
S△ABC,这样的点P有几个请直接写出它们的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从-3、-1、![]() 、1、3这五个数中,随机抽取一个数,记为a,则关于x的一次函数y=-x+a的图象与坐标轴围成三角形的面积不超过4的概率为______.
、1、3这五个数中,随机抽取一个数,记为a,则关于x的一次函数y=-x+a的图象与坐标轴围成三角形的面积不超过4的概率为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com