Question

【题目】如图，直线l1∥l2 ， l1和AB的夹角∠DAB=135°，且AB=50mm，求两平行线l1和l2之间的距离．

Answer 1

【答案】解：如图，过点A作AC⊥l2于点C，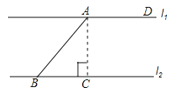

∵直线l1∥l2 ， AC⊥l2 ，
∴∠DAC=90°，
∵∠DAB=135°，
∴∠BAC=∠DAB﹣∠DAC=45°，
∴∠ABC=45°，
∴∠BAC=∠ABC，
∴AC=BC，
在Rt△ABC中，AC2+BC2=AB2 ，
2AC2=502 ，
∴AC=25
∴两平行线l1和l2之间的距离为25．
【解析】过点A作AC⊥l2于点C，证明∠BAC=∠ABC，所以AC=BC，在Rt△ABC中，AC2+BC2=AB2 ， 即可解答．
【考点精析】解答此题的关键在于理解平行线之间的距离的相关知识，掌握两条平行线的距离：两条直线平行，从一条直线上的任意一点向另一条直线引垂线，垂线段的长度，叫做两条平行线的距离．