
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣5,0),对称轴为直线x=﹣2,给出四个结论:①abc>0;②4a+b=0;③若点B(﹣3,y1)、C(﹣4,y2)为函数图象上的两点,则y2<y1;④a+b+c=0.其中,正确结论的个数是( )

A.1B.2C.3D.4
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】某村2016年的人均收入为20000元,2018年的人均收入为24200元
(1)求2016年到2018年该村人均收入的年平均增长率;
(2)假设2019年该村人均收入的增长率与前两年的年平均增长率相同,请你预测2019年村该村的人均收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“绿色生活,美丽家园”号召,某社区计划种植甲、乙两种花卉来美化小区环境.若种植甲种花卉![]() ,乙种花卉
,乙种花卉![]() ,共需430元;种植甲种花卉
,共需430元;种植甲种花卉![]() ,乙种花卉
,乙种花卉![]() ,共需260元.
,共需260元.
(1)求:该社区种植甲种花卉![]() 和种植乙种花卉
和种植乙种花卉![]() 各需多少元?
各需多少元?
(2)该社区准备种植两种花卉共![]() 且费用不超过6300元,那么社区最多能种植乙种花卉多少平方米?
且费用不超过6300元,那么社区最多能种植乙种花卉多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的.正常水位时,大孔水面宽度为![]() ,顶点距水面
,顶点距水面![]() ,小孔顶点距水面
,小孔顶点距水面![]() .当水位上涨刚好淹没小孔时,大孔的水面宽度为________
.当水位上涨刚好淹没小孔时,大孔的水面宽度为________![]() .
.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=-
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=-![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
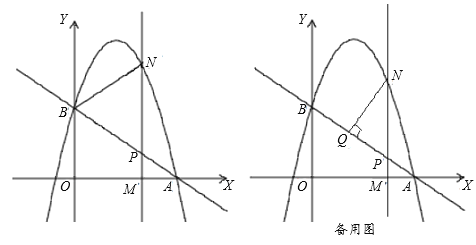
(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①点M在线段OA上运动,若△BPN∽△APM,求点M的坐标;
②过点N作NQ⊥AB于Q,当N点坐标是多少时,NQ取得最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示.下列结论:①abc>0;②2a﹣b<0;③4a﹣2b+c<0;④(a+c)2<b2其中正确的个数有( )
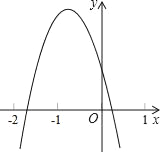
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
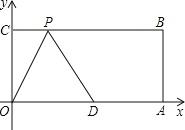
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为![]() 、
、![]() ,点D是OA的中点,点P在BC边上运动,当
,点D是OA的中点,点P在BC边上运动,当![]() 是等腰三角形时,点Р的坐标为_______________.
是等腰三角形时,点Р的坐标为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形MNKO和正六边形ABCDEF边长均为1,把正方形放在正六边形外边,使OK边与AB边重合,如图所示.按下列步骤操作: 将正方形在正六边形外绕点B顺时针旋转,使KN边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使NM边与CD边重合,完成第二次旋转;……在这样连续6次旋转的过程中,点M在图中直角坐标系中的纵坐标可能是( )
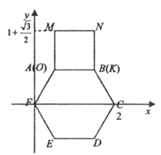
A. 2.2B. -2.2C. 2.3D. -2.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com