【题目】为响应“绿色生活，美丽家园”号召，某社区计划种植甲、乙两种花卉来美化小区环境．若种植甲种花卉
，乙种花卉
，共需430元；种植甲种花卉
，乙种花卉，共需260元．
（1）求：该社区种植甲种花卉和种植乙种花卉各需多少元？
（2）该社区准备种植两种花卉共
且费用不超过6300元，那么社区最多能种植乙种花卉多少平方米？
【答案】（1）该社区种植甲种花卉
需80元，种植乙种花卉需90元；（2）该社区最多能种植乙种花卉
【解析】
（1）设该社区种植甲种花卉需
元，种植乙种花卉需
元，根据“若种植甲种花卉
，乙种花卉
，共需430元；种植甲种花卉，乙种花卉，共需260元”，即可得出关于，的二元一次方程组，解之即可得出结论；
（2）设该社区种植乙种花卉
，则种植甲种花卉
，根据总费用
种植甲种花卉的费用+种植乙种花卉的费用，结合总费用不超过6300元，即可得出关于
的一元一次不等式，解之取其中的最大值即可得出结论．
（1）设该社区种植甲种花卉需元，种植乙种花卉需元，
依题意，得：
，
解得：
．
答：该社区种植甲种花卉需80元，种植乙种花卉需90元．
（2）设该社区种植乙种花卉，则种植甲种花卉，
依题意，得：
，
解得：
，
答：该社区最多能种植乙种花卉.
科目：初中数学 来源： 题型：
【题目】赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如图所示，若这四个全等直角三角形的两条直角边分别平行于x轴和y轴，大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣
上，顶点D1、D2、D3、…、Dn在x轴上，则第n个阴影小正方形的面积为__．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=x2
2x+c的顶点A在直线l：y=x
5上．
（1）求抛物线顶点A的坐标；
（2）设抛物线与y轴交于点B，与x轴交于点C、D（C点在D点的左侧），试判断△ABD的形状；
（3）在直线l上是否存在一点P，使以点P、A、B、D为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
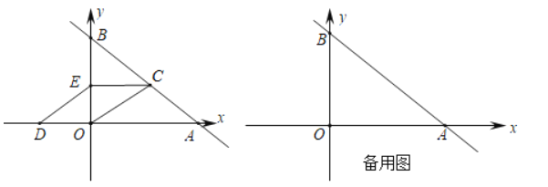
【题目】在平面直角坐标系中，直线y＝kx+4（k≠0）交x轴于点A（8，0），交y轴于点B，
（1）k的值是 ；
（2）点C是直线AB上的一个动点，点D和点E分别在x轴和y轴上．
①如图，点E为线段OB的中点，且四边形OCED是平行四边形时，求OCED的周长；
②当CE平行于x轴，CD平行于y轴时，连接DE，若△CDE的面积为
，请直接写出点C的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在 Rt△ABC 中，∠C＝90°，以 BC 为直径的⊙O 交 AB 于点 D，过点 D 作∠ADE＝∠A，交 AC 于点 E．
（1）求证：DE 是⊙O 的切线；
（2）若
，BC=15cm,求 DE 的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y=ax2+bx+c（a>0）的对称轴为直线x=-1，与x轴的一个交点为（x1，0），且0<x1<1，下列结论：①9a-3b+c>0；②b＜c；③3a+c>0，其中正确结论两个数有______。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是二次函数y＝ax2+bx+c图象的一部分，图象过点A(﹣5，0)，对称轴为直线x＝﹣2，给出四个结论：①abc＞0；②4a+b＝0；③若点B(﹣3，y1)、C(﹣4，y2)为函数图象上的两点，则y2＜y1；④a+b+c＝0．其中，正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC的顶点坐标分别为A(0，2)，B(1，0)，C(2，1).若二次函数y=x2+bx+1的图像与阴影部分(含边界)一定有公共点，则实数b的取值范围是( )
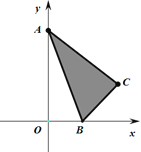
A. b≤-2B. b<-2C. b≥-2D. b>-2
查看答案和解析>>
科目：初中数学 来源： 题型：
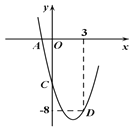
【题目】二次函数
的部分图象如图所示，其中图象与x轴交于点A（－1,0），与y轴交于点C（0，－5），且经过点D（3，－8）.（1）求此二次函数的解析式； （2）用配方法将将此二次函数的解析式写成
的形式，并直接写出此二次函数图象的顶点坐标以及它与x轴的另一个交点B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com