
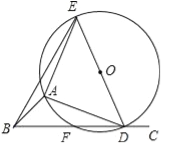
【题目】如图,∠ABC=45°,△ADE是等腰直角三角形,AE=AD,顶点A、D分别再∠ABC的两边BA、BC上滑动(不与点B重合),△ADE的外接圆交BC于点F,O为圆心.
(1)直接写出∠AFE的度数;
(2)当点D在点F的右侧时,①求证:EF﹣DF=![]() AF;
AF;
②若AB=![]() ,
,![]() <BE≤
<BE≤![]() ,求⊙O的面积S的取值范围.
,求⊙O的面积S的取值范围.
【答案】(1)45°;(2)①证明见解析;②16π<S<40π.
【解析】
试题分析:(1)根据等腰直角三角形的性质和圆周角定理即可得到结论;
(2)①根据已知条件得到AB=AF,∠BAF=90°推出△ABD≌△AFE,根据全等三角形的性质得到BD=EF,由线段的和差得到EF﹣DF=BD﹣DF=BF,根据三角函数的定义得到BF=![]() AF,即可得到结论;
AF,即可得到结论;
②由(2)①得BD=EF,根据已知条件得到BF=8,根据勾股定理得到![]() <BE≤
<BE≤![]() ,求得8<EF<12,于是得到S=
,求得8<EF<12,于是得到S=![]() (x﹣4)2+8π,根据二次函数的性质即可得到结论.
(x﹣4)2+8π,根据二次函数的性质即可得到结论.
试题解析:(1)∠AFE=45°,连接AF,∵△ADE是等腰直角三角形,∴∠AFE=∠EDF=45°;
(2)①连接EF,∵∠EFD=∠EAD=90°,∴∠BFE=90°,∵∠AFE=45°,∴∠AFB=∠AFE=45°,∴AB=AF,∠BAF=90°,∴∠BAD=∠FAE,在△ABD和△AFE中,∵AD=AE,∠BAD=∠FAE,AB=AF,∴△ABD≌△AFE,∴BD=EF,∴EF﹣DF=BD﹣DF=BF,∵AF=BFcos∠AFB=![]() BF,即BF=
BF,即BF=![]() AF,∴EF﹣DF=
AF,∴EF﹣DF=![]() AF;
AF;
②由(2)①得BD=EF,∵∠BAF=90°,AB=![]() ,∴BF=
,∴BF=![]() =
=![]() =8,设BD=x,则EF=x,DF=x﹣8,∵BE2=EF2+BF2,
=8,设BD=x,则EF=x,DF=x﹣8,∵BE2=EF2+BF2,![]() <BE≤
<BE≤![]() ,∴128<EF2+82<208,∴8<EF<12,即8<x<12,∴S=
,∴128<EF2+82<208,∴8<EF<12,即8<x<12,∴S=![]() DE2=
DE2=![]() [x2+(x﹣8)2]=
[x2+(x﹣8)2]=![]() (x﹣4)2+8π,∵
(x﹣4)2+8π,∵![]() >0,∴抛物线的开口向上,∵抛物线的对称轴为直线x=4,∴当8<x<12时,S随x的增大而增大,∴16π<S<40π.
>0,∴抛物线的开口向上,∵抛物线的对称轴为直线x=4,∴当8<x<12时,S随x的增大而增大,∴16π<S<40π.



科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红枣丰收了,为了运输方便,小华的爸爸打算把一个长为(a+2b)cm、宽为(a+b)cm的长方形纸板制成一个有底无盖的盒子,在长方形纸板的四个角各截去一个边长为 ![]() bcm的小正方形,然后沿折线折起即可,如图所示,现将盒子的外表面贴上彩色花板.
bcm的小正方形,然后沿折线折起即可,如图所示,现将盒子的外表面贴上彩色花板. 
(1)则至少需要彩纸的面积是多少?
(2)当a=8,b=6时,求至少需要彩纸的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD的两条边在坐标轴上,点D与坐标原点O重合,且AD=8,AB=6.如图2,矩形ABCD沿OB方向以每秒1个单位长度的速度运动,同时点P从A点出发也以每秒1个单位长度的速度沿矩形ABCD的边AB经过点B向点C运动,当点P到达点C时,矩形ABCD和点P同时停止运动,设点P的运动时间为t秒.

(1)当t=5时,请直接写出点D、点P的坐标;
(2)当点P在线段AB或线段BC上运动时,求出△PBD的面积S关于t的函数关系式,并写出相应t的取值范围;
(3)点P在线段AB或线段BC上运动时,作PE⊥x轴,垂足为点E,当△PEO与△BCD相似时,求出相应的t值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com