
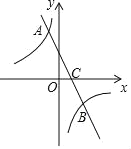
【题目】如图,直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)交于点A(
(m≠0)交于点A(![]() ,2)B(1,﹣1).
,2)B(1,﹣1).
(1)方程kx+b﹣![]() =0的解为 ,不等式
=0的解为 ,不等式![]() 的解集是 ;(请直接写出答案)
的解集是 ;(请直接写出答案)
(2)点P在x轴上,如果S△ABP=3,求点P的坐标.
【答案】(1)x=﹣![]() 或1;﹣
或1;﹣![]() <x<0或x>1;(2)点P的坐标为(﹣
<x<0或x>1;(2)点P的坐标为(﹣![]() ,0)或(
,0)或(![]() ,0).
,0).
【解析】
(1)结合图象,分析函数值的大小关系即可;(2)用待定系数法求直线解析式;设点P的坐标为(x,0),则PC=|x﹣![]() |,根据面积公式求解.
|,根据面积公式求解.
解:(1)当x=﹣![]() 或x=1时,kx+b=
或x=1时,kx+b=![]() ,所以方程kx+b﹣
,所以方程kx+b﹣![]() =0的解为x=﹣
=0的解为x=﹣![]() 或1;
或1;
当﹣![]() <x<0或x>1时,kx+b<
<x<0或x>1时,kx+b<![]() ,则不等式kx+b<
,则不等式kx+b<![]() 的解集是﹣
的解集是﹣![]() <x<0或x>1;
<x<0或x>1;
故答案为x=﹣![]() 或1;﹣
或1;﹣![]() <x<0或x>1;
<x<0或x>1;
(2)把A(![]() ,2)B(1,﹣1)代入y=kx+b得
,2)B(1,﹣1)代入y=kx+b得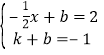 ,解得
,解得![]() ,则直线解析式为y=﹣2x﹣1,
,则直线解析式为y=﹣2x﹣1,
当x=0时,﹣2x+1=0,解得x=![]() ,则C(
,则C(![]() ,0),
,0),
设点P的坐标为(x,0),则PC=|x﹣![]() |,
|,
∵S△ABP=3,
∴![]() ×3|x﹣
×3|x﹣![]() |=3,即|x﹣
|=3,即|x﹣![]() |=2,
|=2,
解得:x1=﹣![]() ,x2=
,x2=![]() ,
,
∴点P的坐标为(﹣![]() ,0)或(
,0)或(![]() ,0).
,0).


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
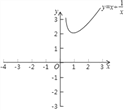
【题目】某数学兴趣小组对函数y=x+![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
x | … | ﹣3 | ﹣2 | ﹣1 | - | - |
|
| 1 | 2 | 3 | … |
y | … | - | m | ﹣2 | - | - |
|
| 2 |
|
| … |
(1)自变量x的取值范围是 ,m= .
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现:
①方程x+![]() =3有 个实数根;
=3有 个实数根;
②若关于x的方程x+![]() =t有2个实数根,则t的取值范围是 .
=t有2个实数根,则t的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为方便市民出行,减轻城市中心交通压力,贵阳市地铁1号线于2018年12月1号正式全线开通.地铁开通后,李明爸爸妈妈的出行方式将由乘公交车改为乘坐地铁,爸爸从国际生态会议中心站出发至喷水池站,每天所需的时间将比以往节省70%;妈妈从国际生态会议中心站出发至珠江路站,每天所需的时间将比以往节省55%,这样两人所需的时间共节省60%,现在两人乘地铁所需的时间之和为1.2小时.请问李明爸爸妈妈原来乘公交车上班时每天所需时间各为多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
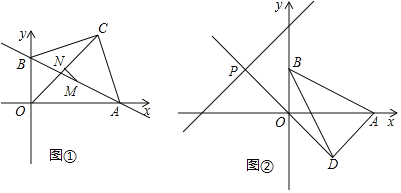
【题目】如图1,在平面直角坐标系中,直线![]() 与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.
与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.
(1)直接写出![]() = ;
= ;
(2)请你过点C作CE⊥y轴于E点,试探究OB+OA与CE的数量关系,并证明你的结论;
(3)若点M为AB的中点,点N为OC的中点,求MN的值;
(4)如图2,将线段AB绕点B沿顺时针方向旋转至BD,且OD⊥AD,延长DO交直线![]() 于点P,求点P的坐标.
于点P,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在以点O为原点的数轴上,点A表示的数是3,点B在原点的左侧,且AB=6AO(我们把数轴上两点之间的距离用表示两点的大写字母一起标记,比如,点A与点B之间的距离记作AB).
(1)B点表示的数是_______.
(2)若动点P从O点出发,以每秒2个单位长度的速度匀速向左运动,问经过几秒钟后PA=3PB?并求出此时P点在数轴上对应的数.
(3)若动点M.P.N分别同时从A、O、B出发,匀速向右运动,其速度分别为1个单位长度/秒.2个单位长度/秒.4个单位长度/秒,设运动时间为t秒,请直接写出PM.PN.MN中任意两个相等时的时间.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 到点
到点![]() ,点
,点![]() 的距离相等,动点
的距离相等,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向右匀速运动,设运动的时间为
个单位长度的速度沿数轴向右匀速运动,设运动的时间为![]() (
(![]() )秒.
)秒.

(1)点![]() 表示的数是 .
表示的数是 .
(2)点![]() 表示的数是 .(用含有
表示的数是 .(用含有![]() 的代数式表示);
的代数式表示);
(3)求当![]() 等于多少秒时,点
等于多少秒时,点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() 个单位长度.
个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 是最大的负整数,且
是最大的负整数,且![]() 、
、![]() 满足
满足![]() 与
与![]() 互为相反数.
互为相反数.
![]()
(1)![]() ______,
______,![]() ______,
______,![]() ______.
______.
(2)若将数轴折叠,使得![]() 点与
点与![]() 点重合,则点
点重合,则点![]() 与数______表示的点重合;
与数______表示的点重合;
(3)点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒2个单位长度的速度向左运动,同时,点
以每秒2个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒1个单位长度和3个单位长度的速度向右运动,假设
分别以每秒1个单位长度和3个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() .
.
①请问:![]() 的值是否随着时间
的值是否随着时间![]() 变化而改变?若变化,说明理由;若不变,请求其值.
变化而改变?若变化,说明理由;若不变,请求其值.
②探究:在(3)的情况下,若点![]() 、
、![]() 向右运动,点
向右运动,点![]() 向左运动,速度保持不变,
向左运动,速度保持不变,![]() 值是否随着时间
值是否随着时间![]() 的变化而改变,若变化,请说明理由;若不变,请求其值.
的变化而改变,若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=x-2y,B=-x-4y+1.
(1)求2(A+B)-(A-B);(结果用含x,y的代数式表示)
(2)当![]() 与
与![]() 互为相反数时,求(1)中代数式的值.
互为相反数时,求(1)中代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上有两点A、B,它们对应的数分别为a、b,其中a=12.
![]()
(1)在点B的左侧作线段BC=AB,在B的右侧作线段BD=3AB(要求:作出图形,不写作法,保留作图痕迹);
(2)若点C对应的数为c,点D对应的数为的d,且AB=20,求c、d的值;
(3)在(2)的条件下,设点M是BD的中点,N是数轴上一点,且CN=2DN,请直接写出MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com