
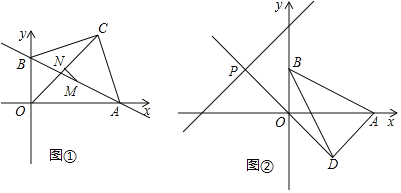
【题目】如图1,在平面直角坐标系中,直线![]() 与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.
与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.
(1)直接写出![]() = ;
= ;
(2)请你过点C作CE⊥y轴于E点,试探究OB+OA与CE的数量关系,并证明你的结论;
(3)若点M为AB的中点,点N为OC的中点,求MN的值;
(4)如图2,将线段AB绕点B沿顺时针方向旋转至BD,且OD⊥AD,延长DO交直线![]() 于点P,求点P的坐标.
于点P,求点P的坐标.
【答案】(1) 4;(2)OB+OA=2CE;见解析;(3)MN=![]() ;(4)P(
;(4)P(![]() ,
,![]() ).
).
【解析】
(1)令x=0,求出y的值,令y=0,求出x的值,即可得出OA,OB的长,根据三角形面积公式即可求出结果;
(2)过点C作CF⊥x轴,垂足为点F,易证△CEB≌△CFA与四边形CEOF是正方形,从而得AF=BE,CE=BE=OF,由OB=OE-BE,AO=OF+AF可得结论;
(3)求出C点坐标,利用中点坐标公式求出点M,N的坐标,进而用两点间的距离公式求解即可得出结论;
(4)先判断出点B是AQ的中点,进而求出Q的坐标,即可求出DP的解析式,联立成方程组求解即可得出结论.
(1)∵直线y=-![]() x+2交坐标轴于A,B两点,
x+2交坐标轴于A,B两点,
令x=0,则y=2,令y=0,则x=4,
∴BO=2,AO=4,
∴![]() =
=![]() ;
;
(2)作CF⊥x轴于F,作CE⊥y轴于E,如图,
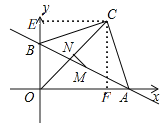
∴∠BFC=∠AEC=90°
∵∠EOF=90°,
∴四边形OECF是矩形,
∴CF=OE,CE=OF,∠ECF=90°,
∵∠ACB=90°
∴∠BCF=∠ACE,
∵BC=AC,
∴△CFB≌△CEA,
∴CF=CE,AF=BE,
∴四边形OECF是正方形,
∴OE=OF=CE=CF,
∴OB=OE-BE,OA=OF+AF,
∴OB+OA=OE+OF=2CE;
(3)由(2)得CE=3,
∴OE=3,
∴OF=3,
∴C(3,3);
∵M是线段AB的中点,而A(4,0),B(0,2),
∴M(2,1),
同理:N(![]() ,
,![]() ),
),
∴MN=![]() ;
;
(3)如图②延长AB,DP相交于Q,
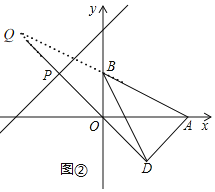
由旋转知,BD=AB,
∴∠BAD=∠BDA,
∵AD⊥DP,
∴∠ADP=90°,
∴∠BDA+∠BDQ=90°,∠BAD+∠AQD=90°,
∴∠AQD=∠BDQ,∴BD=BQ,
∴BQ=AB,
∴点B是AQ的中点,
∵A(4,0),B(0,2),
∴Q(-4,4),
∴直线DP的解析式为y=-x①,
∵直线DO交直线y=x+5②于P点,
联立①②解得,x=-![]() ,y=
,y=![]() ,
,
∴P(-![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】已知数轴上有![]() 三点分别表示数
三点分别表示数![]() ,且
,且![]() 满足
满足![]()
![]() .两只电子蚂蚁甲、乙分别从
.两只电子蚂蚁甲、乙分别从![]() 两点同时出发相向而行,若甲的速度为
两点同时出发相向而行,若甲的速度为![]() 个单位/秒,乙的速度为
个单位/秒,乙的速度为![]() 个单位/秒.
个单位/秒.
(1)求![]() 的值并在数轴上标出
的值并在数轴上标出![]() 三点.
三点.

(2)问甲、乙在数轴上的哪个点相遇?
(3)问多少秒后,甲到![]() 的距离为
的距离为![]() 个单位?
个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P是菱形ABCD的对角线AC上的一个动点,已知AB=1,∠ADC=120°, 点M,N分别是AB,BC边上的中点,则△MPN的周长最小值是______.
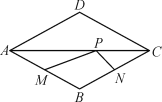
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区. 已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市. 已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从C市运往B市的救灾物资为x吨.
(1)请填写下表;

(2)设C、D两市的总运费为W元,求W与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从C市到B市的路况得到了改善,缩短了运输时间,运费每吨减少n元(n>0),其余路线运费不变,若C、D两市的总运费的最小值不小于10080元,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国移动公司开设适合普通用户的两种通讯业务分别是:“全球通”用户先缴![]() 元月租,然后每分钟通话费用
元月租,然后每分钟通话费用![]() 元;“神州行”用户不用缴纳月租费,每分钟通话
元;“神州行”用户不用缴纳月租费,每分钟通话![]() 元.(通话均指拨打本地电话)
元.(通话均指拨打本地电话)
![]() 设一个月内通话时间约为
设一个月内通话时间约为![]() 分钟(
分钟(![]() 且
且![]() 为整数),求这两种用户每月需缴的费用分别是多少元?(用含
为整数),求这两种用户每月需缴的费用分别是多少元?(用含![]() 的式子表示)
的式子表示)
![]() 若张老师一个月通话约
若张老师一个月通话约![]() 分钟,请你给他提个建议,应选择哪种移动通讯方式合算一些?并说明理由.
分钟,请你给他提个建议,应选择哪种移动通讯方式合算一些?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
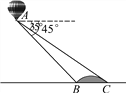
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.
(结果保留整数,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
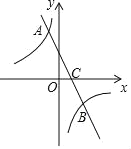
【题目】如图,直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)交于点A(
(m≠0)交于点A(![]() ,2)B(1,﹣1).
,2)B(1,﹣1).
(1)方程kx+b﹣![]() =0的解为 ,不等式
=0的解为 ,不等式![]() 的解集是 ;(请直接写出答案)
的解集是 ;(请直接写出答案)
(2)点P在x轴上,如果S△ABP=3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加射箭比赛,两人各射了5箭,他们的成绩(单位:环)统计如下表.
第1箭 | 第2箭 | 第3箭 | 第4箭 | 第5箭 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 6 | 5 | 7 |
(1)分别计算甲、乙两人射箭比赛的平均成绩;
(2)你认为哪个人的射箭成绩比较稳定?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题.
我们知道,|x|=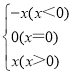 .现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x-2|时,可令x+1=0和x-2=0,分别求得x=-1,x=2(称-1,2分别为|x+1|与|x-2|的零点值).在实数范围内,零点值x=-1和x=2可将全体实数分成不重复且不遗漏的如下3种情况:
.现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x-2|时,可令x+1=0和x-2=0,分别求得x=-1,x=2(称-1,2分别为|x+1|与|x-2|的零点值).在实数范围内,零点值x=-1和x=2可将全体实数分成不重复且不遗漏的如下3种情况:
(1)x<-1;
(2)-1≤x<2;
(3)x≥2.
从而化简代数式|x+1|+|x-2|可分以下3种情况:
(1)当x<-1时,原式=-(x+1)-(x-2)=-2x+1;
(2)当-1≤x<2时,原式=x+1-(x-2)=3;
(3)当x≥2时,原式=x+1+x-2=2x-1.
综上讨论,原式=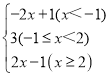
通过以上阅读,请你解决以下问题:
(1)分别求出|x+3|和|x-5|的零点值;
(2)化简|x+3|+|x-5|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com