
【题目】某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区. 已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市. 已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从C市运往B市的救灾物资为x吨.
(1)请填写下表;

(2)设C、D两市的总运费为W元,求W与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从C市到B市的路况得到了改善,缩短了运输时间,运费每吨减少n元(n>0),其余路线运费不变,若C、D两市的总运费的最小值不小于10080元,求n的取值范围.
【答案】(1)如表见解析;(2)W=-10x+13200,![]() ; (3)
; (3)![]()
【解析】
(1)根据题意可以将表格中的空缺数据补充完整;
(2)根据题意可以求得w与x的函数关系式,并写出x的取值范围;
(3)根据题意,利用分类讨论的数学思想可以解答本题.
(1)∵C市运往B市x吨,
∴C市运往A市(240-x)吨,D市运往B市(300-x)吨,D市运往A市260-(300-x)=(x-40)吨,
故答案为:240-x、x-40、300-x;
(2)由题意可得,
w=20(240-x)+25x+15(x-40)+30(300-x)=-10x+13200,
又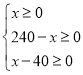 得40≤x≤240,
得40≤x≤240,
∴w=10x+13200(40≤x≤240);
(3)由题意可得,
w=20(240-x)+(25-n)x+15(x-40)+30(300-x)=-(n+10)x+13200,
∵n>0,
∴-(n+10)<0,
∴W随x的增大而减小
当x取最大值240时,W最小值=-(n+10)×240+13200≥10080,
即:-(n+10)×240+13200≥10080
解得,n≤3,
由上可得,m的取值范围是0<n≤3.


科目:初中数学 来源: 题型:
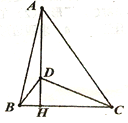
【题目】如图在△ABC中,AH⊥BC于点H,在AH上取一点D,连接DC,使DA=DC,且∠ADC=2∠DBC,若DH=2,BC=6,则AB=_________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题:我们知道|x|=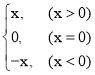 ,现在我们可以用这个结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别叫做|x+1|与|x﹣2|的零点值.)在有理数范围内,零点值x=﹣1和x=2可将全体有理数分成不重复且不遗漏的如下3种情况:
,现在我们可以用这个结论来化简含有绝对值的代数式,如化简代数式|x+1|+|x﹣2|时,可令x+1=0和x﹣2=0,分别求得x=﹣1,x=2(称﹣1,2分别叫做|x+1|与|x﹣2|的零点值.)在有理数范围内,零点值x=﹣1和x=2可将全体有理数分成不重复且不遗漏的如下3种情况:
(1)当x<﹣1时,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
(2)当﹣1≤x≤2时,原式=x+1﹣(x﹣2)=3;
(3)当x>2时,原式=x+1+x﹣2=2x﹣1.
综上所述,原式=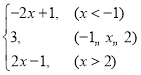 .
.
通过以上阅读,请你解决以下问题:
(1)分别求出|x+2|和|x﹣4|的零点值;
(2)化简代数式|x+2|+|x﹣4|;
(3)求方程:|x+2|+|x﹣4|=6的整数解;
(4)|x+2|+|x﹣4|是否有最小值?如果有,请直接写出最小值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.
(1)以x(单位:元)表示商品原价,y(单位:元)表示购物金额,分别就两家商场的让利方式写出y关于x的函数解析式;
(2)在同一直角坐标系中画出(1)中函数的图象;
(3)春节期间如何选择这两家商场去购物更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为方便市民出行,减轻城市中心交通压力,贵阳市地铁1号线于2018年12月1号正式全线开通.地铁开通后,李明爸爸妈妈的出行方式将由乘公交车改为乘坐地铁,爸爸从国际生态会议中心站出发至喷水池站,每天所需的时间将比以往节省70%;妈妈从国际生态会议中心站出发至珠江路站,每天所需的时间将比以往节省55%,这样两人所需的时间共节省60%,现在两人乘地铁所需的时间之和为1.2小时.请问李明爸爸妈妈原来乘公交车上班时每天所需时间各为多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将口ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
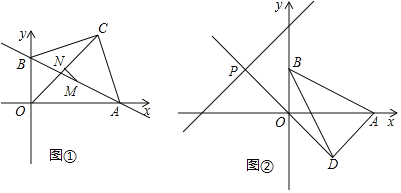
【题目】如图1,在平面直角坐标系中,直线![]() 与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.
与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.
(1)直接写出![]() = ;
= ;
(2)请你过点C作CE⊥y轴于E点,试探究OB+OA与CE的数量关系,并证明你的结论;
(3)若点M为AB的中点,点N为OC的中点,求MN的值;
(4)如图2,将线段AB绕点B沿顺时针方向旋转至BD,且OD⊥AD,延长DO交直线![]() 于点P,求点P的坐标.
于点P,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 到点
到点![]() ,点
,点![]() 的距离相等,动点
的距离相等,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向右匀速运动,设运动的时间为
个单位长度的速度沿数轴向右匀速运动,设运动的时间为![]() (
(![]() )秒.
)秒.

(1)点![]() 表示的数是 .
表示的数是 .
(2)点![]() 表示的数是 .(用含有
表示的数是 .(用含有![]() 的代数式表示);
的代数式表示);
(3)求当![]() 等于多少秒时,点
等于多少秒时,点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() 个单位长度.
个单位长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com