
����Ŀ��Ϊ�����������,����������Ľ�ͨѹ��,�����е���1������2018��12��1����ʽȫ�߿�ͨ.������ͨ�������ְ�����ij��з�ʽ���ɳ˹�������Ϊ��������,�ְִӹ�����̬��������վ��������ˮ��վ��ÿ�������ʱ�佫��������ʡ70%������ӹ�����̬��������վ�������齭·վ��ÿ�������ʱ�佫��������ʡ55%���������������ʱ�乲��ʡ60%,�������˳˵��������ʱ��֮��Ϊ1.2Сʱ.���������ְ�����ԭ���˹������ϰ�ʱÿ������ʱ���Ϊ����Сʱ��
���𰸡������ְ�����ԭ���˹������ϰ�ʱÿ������ʱ��ֱ�Ϊ1Сʱ��2Сʱ.
��������
��ְ�ԭ������ʱ��ΪxСʱ���������ͨ���裨1-70%��xСʱ������ԭ������ʱ��ΪyСʱ���������ͨ���裨1-55%��yСʱ��������Ŀ�еĵ�����ϵ�г������飬�ⷽ���鼴��.
�⣺��ְ�ԭ������ʱ��ΪxСʱ���������ͨ���裨1-70%��xСʱ������ԭ������ʱ��ΪyСʱ���������ͨ���裨1-55%��yСʱ����������ã�
![]()
��ã�![]()
�������ְ�����ԭ���˹������ϰ�ʱÿ������ʱ��ֱ�Ϊ1Сʱ��2Сʱ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ȤС��Ϊ���˽ⱾУѧ���μӿ���������������������ȡ��У40��ѧ�������ʾ����飬ͳ�����������������������в�������ͳ��ͼ��

����������Ϣ����������⣺
��1�����������������ͳ��ͼ�У��������μ�������Ӧ��Բ�ĽǵĶ���Ϊ ���������μӿ�������������ѧ����ϲ����һ����Ŀ���У�ϲ������������� �ˣ���ȫ����ͳ��ͼ��
��2����У����1200��ѧ���������ȫУѧ���о����μӿ�������������ϲ������Ŀ��ƹ����������ж����ˣ�
��3��������ƹ��������������������������������ë������Ŀ����ѡ������Ŀ������ȤС�飬�����б�������״ͼ�ķ�����ǡ��ѡ����ƹ������������������������Ŀ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⣮
��1���ϲ�����ͬ��� 4a2��3b2��2ab��4a2��3b2��5ba
��2���Ȼ�������ֵ��2��3x2��4xy����4��2x2��3xy��1��������|x��1|+��y+2��2=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P������ABCD�ĶԽ���AC�ϵ�һ�����㣬��֪AB=1����ADC=120��, ��M��N�ֱ���AB��BC���ϵ��е㣬����MPN���ܳ���Сֵ��______.
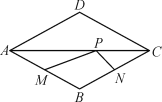
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���ƽ��ֱ������ϵ�У��ȱߡ�ABC�Ķ���A��B������ֱ�Ϊ��5��0������9��0������D��x����������һ�����㣬����CD������ACD�Ƶ�C��ʱ����ת60���õ���BCE������DE��
������ֱ��д����C�����꣬���жϡ�CDE����״��˵�����ɣ�
��������ͼ�ڣ�����D���߶�AB���˶�ʱ����BDE���ܳ��Ƿ������Сֵ�������ڣ������BDE����С�ܳ�����ʱ��D�����ꣻ�������ڣ�˵�����ɣ�
����������BDE��ֱ��������ʱ�����D�����꣮��ֱ��д��������ɣ�
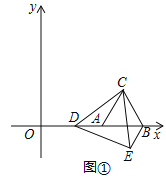
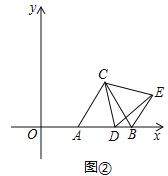
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��5�£��ҹ��Ϸ�ijʡA��B�����������غ����ֺ���1.5���˱���ת�ƣ��ڽ�����C��D��֪A��B���зֱ����������200�ֺ�300�ֵ���Ϣ������������֧Ԯ����. ��֪C���о�������240�֣�D���о�������260�֣��ֽ���Щ��������ȫ������A��B����. ��֪��C������A��B���еķ��÷ֱ�Ϊÿ��20Ԫ��25Ԫ����D��������A��B���еķ��÷ֱ�Ϊÿ��15Ԫ��30Ԫ�����C������B�еľ�������Ϊx��.
(1)��������

(2)��C��D���е����˷�ΪWԪ����W��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
(3)�������ޣ���C�е�B�е�·���õ��˸��ƣ�����������ʱ�䣬�˷�ÿ�ּ���nԪ��n>0��������·���˷Ѳ��䣬��C��D���е����˷ѵ���Сֵ��С��10080Ԫ����n��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й��ƶ���˾�����ʺ���ͨ�û�������ͨѶҵ��ֱ��ǣ���ȫ��ͨ���û��Ƚ�![]() Ԫ���⣬Ȼ��ÿ����ͨ������
Ԫ���⣬Ȼ��ÿ����ͨ������![]() Ԫ�������������û����ý�������ѣ�ÿ����ͨ��
Ԫ�������������û����ý�������ѣ�ÿ����ͨ��![]() Ԫ����ͨ����ָ���ص绰��
Ԫ����ͨ����ָ���ص绰��
![]() ��һ������ͨ��ʱ��ԼΪ
��һ������ͨ��ʱ��ԼΪ![]() ���ӣ�
���ӣ�![]() ��
��![]() Ϊ�����������������û�ÿ����ɵķ��÷ֱ��Ƕ���Ԫ�����ú�
Ϊ�����������������û�ÿ����ɵķ��÷ֱ��Ƕ���Ԫ�����ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
![]() ������ʦһ����ͨ��Լ
������ʦһ����ͨ��Լ![]() ���ӣ��������������飬Ӧѡ�������ƶ�ͨѶ��ʽ����һЩ����˵�����ɣ�
���ӣ��������������飬Ӧѡ�������ƶ�ͨѶ��ʽ����һЩ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��kx+b��k��0����˫����y��![]() ��m��0�����ڵ�A��
��m��0�����ڵ�A��![]() ��2��B��1����1����
��2��B��1����1����
��1������kx+b��![]() ��0�Ľ�Ϊ�� ��������ʽ
��0�Ľ�Ϊ�� ��������ʽ![]() �Ľ⼯���� ��������ֱ��д���𰸣�
�Ľ⼯���� ��������ֱ��д���𰸣�
��2����P��x���ϣ����S��ABP��3�����P�����꣮
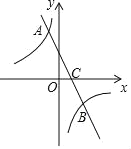
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ֱ֪��AB�ĺ�������ʽΪy=��2x+8����x�ύ�ڵ�A����y�ύ�ڵ�B��
��1����A��B��������ꣻ
��2������P��m��n��Ϊ�߶�AB�ϵ�һ�����㣨��A��B���غϣ�����PE��x���ڵ�E��PF��y���ڵ�F������EF���ʣ�
������PAO�����ΪS����S����m�ĺ�����ϵʽ����д��m��ȡֵ��Χ��
���Ƿ���ڵ�P��ʹEF��ֵ��С�������ڣ����EF����Сֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com