
【题目】如图在△ABC中,AH⊥BC于点H,在AH上取一点D,连接DC,使DA=DC,且∠ADC=2∠DBC,若DH=2,BC=6,则AB=_________________。
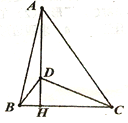
【答案】![]()
【解析】
如图,过点B作BE∥DH,并在BE上取BE=2DH,连接ED,EC.并取BE的中点K,连接DK,根据垂直的定义得到∠DHC=90°,由平行线的性质得到∠EBC=90°.由线段垂直平分线的性质得到BK=DH.推出四边形DKBH为矩形,得到DK⊥BE,根据等腰三角形的性质得到DE=DB,∠EDB=2∠KDB,通过△EDC≌△BDA,得到AB=CE,根据勾股定理得到![]() ,于是得到结论.
,于是得到结论.
解:如图,过点B作BE∥DH,并在BE上取BE=2DH,连接ED,EC.并取BE的中点K,连接DK,
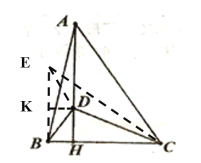
∵DH⊥BC于H,
∴∠DHC=90°,
∵BE∥DH,
∴∠EBC=90°,
∵∠EBC=90°,
∵K为BE的中点,BE=2DH,
∴BK=DH.
∵BK∥DH,
∴四边形DKBH为矩形,DK∥BH,
∴DK⊥BE,∠KDB=∠DBC,
∴DE=DB,∠EDB=2∠KDB,
∵∠ADC=2∠DBC,
∴∠EDB=∠ADC,
∴∠EDB+∠EDA=∠ADC+∠EDA,即∠EDC=∠BDA,
在△EDC、△BDA中,
 ,
,
∴△EDC≌△BDA,
∴AB=CE,
∴![]() ,
,
∴AB=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6,且ABCD的周长为40,则ABCD的面积为( )
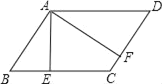
A. 24B. 36C. 40D. 48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1中ΔABC是等边三角形,DE是中位线,F是线段BC延长线上一点,且CF=AE,连接BE,EF.
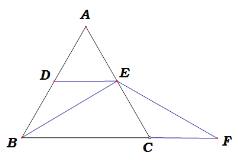
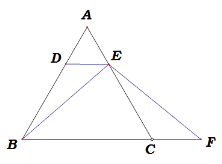
图1 图2
(1)求证:BE=EF;
(2)若将DE从中位线的位置向上平移,使点D、E分别在线段AB、AC上(点E与点A不重合),其他条件不变,如图2,则(1)题中的结论是否成立?若成立,请证明;若不成立.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组为了了解本校学生参加课外体育锻炼情况,随机抽取本校40名学生进行问卷调查,统计整理并绘制了如下两幅尚不完整的统计图:

根据以上信息解答下列问题:
(1)课外体育锻炼情况统计图中,“经常参加”所对应的圆心角的度数为 ;“经常参加课外体育锻炼的学生最喜欢的一种项目”中,喜欢足球的人数有 人,补全条形统计图.
(2)该校共有1200名学生,请估计全校学生中经常参加课外体育锻炼并喜欢的项目是乒乓球的人数有多少人?
(3)若在“乒乓球”、“篮球”、“足球”、“羽毛球”项目中任选两个项目成立兴趣小组,请用列表法或画树状图的方法求恰好选中“乒乓球”、“篮球”这两个项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
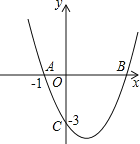
【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 两点,与x轴交于另一点B.
两点,与x轴交于另一点B.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 已知点
已知点![]() 在第四象限的抛物线上,求点D关于直线BC对称的点
在第四象限的抛物线上,求点D关于直线BC对称的点![]() 的坐标.
的坐标.
![]() 在
在![]() 的条件下,连接BD,问在x轴上是否存在点P,使
的条件下,连接BD,问在x轴上是否存在点P,使![]() ?若存在,请求出P点的坐标;若不存在,请说明理由.
?若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有![]() 三点分别表示数
三点分别表示数![]() ,且
,且![]() 满足
满足![]()
![]() .两只电子蚂蚁甲、乙分别从
.两只电子蚂蚁甲、乙分别从![]() 两点同时出发相向而行,若甲的速度为
两点同时出发相向而行,若甲的速度为![]() 个单位/秒,乙的速度为
个单位/秒,乙的速度为![]() 个单位/秒.
个单位/秒.
(1)求![]() 的值并在数轴上标出
的值并在数轴上标出![]() 三点.
三点.

(2)问甲、乙在数轴上的哪个点相遇?
(3)问多少秒后,甲到![]() 的距离为
的距离为![]() 个单位?
个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
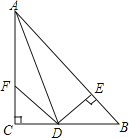
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF,BC=8,AB=10,则△FCD的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区. 已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市. 已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从C市运往B市的救灾物资为x吨.
(1)请填写下表;

(2)设C、D两市的总运费为W元,求W与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从C市到B市的路况得到了改善,缩短了运输时间,运费每吨减少n元(n>0),其余路线运费不变,若C、D两市的总运费的最小值不小于10080元,求n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com