
【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 两点,与x轴交于另一点B.
两点,与x轴交于另一点B.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 已知点
已知点![]() 在第四象限的抛物线上,求点D关于直线BC对称的点
在第四象限的抛物线上,求点D关于直线BC对称的点![]() 的坐标.
的坐标.
![]() 在
在![]() 的条件下,连接BD,问在x轴上是否存在点P,使
的条件下,连接BD,问在x轴上是否存在点P,使![]() ?若存在,请求出P点的坐标;若不存在,请说明理由.
?若存在,请求出P点的坐标;若不存在,请说明理由.
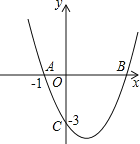
【答案】(1)![]() ;(2)点D关于直线BC对称的点
;(2)点D关于直线BC对称的点![]() ;
;![]() 存在,
存在,![]()
【解析】分析:(1)、将A(-1,0)、C(0,-3)两点坐标代入抛物线![]() 中,列方程组求a、b的值即可;(2)、将点D(m,-m-1)代入(1)中的抛物线解析式,求m的值,再根据对称性求点D关于直线BC对称的点D'的坐标;(3)、当∠PCB=∠CBD时,可知CP∥BD,根据三角形的全等关系确定P点坐标.
中,列方程组求a、b的值即可;(2)、将点D(m,-m-1)代入(1)中的抛物线解析式,求m的值,再根据对称性求点D关于直线BC对称的点D'的坐标;(3)、当∠PCB=∠CBD时,可知CP∥BD,根据三角形的全等关系确定P点坐标.
详解:![]() 将
将![]() 、
、![]() 代入抛物线
代入抛物线![]() 中,
中,
得![]() , 解得
, 解得![]() ,
, ![]() ;
;
![]() 将点
将点![]() 代入
代入![]() 中,得:
中,得:![]() ,
,
解得![]() 或
或![]() ,
, ![]() 点
点![]() 在第四象限,
在第四象限, ![]() ,
,
![]() 直线BC解析式为
直线BC解析式为![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
![]() 点D关于直线BC对称的点
点D关于直线BC对称的点![]() ;
;
![]() 存在
存在![]() 满足条件的点P有两个.
满足条件的点P有两个.
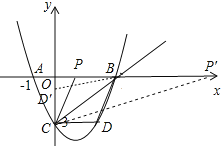
![]() 过点C作
过点C作![]() ,交x轴于P,则
,交x轴于P,则![]() ,
, ![]() 直线BD解析式为
直线BD解析式为![]() ,
,
![]() 直线CP过点C,
直线CP过点C, ![]() 直线CP的解析式为
直线CP的解析式为![]() ,
, ![]() 点P坐标
点P坐标![]() ,
,
![]() 连接
连接![]() ,过点C作
,过点C作![]() ,交x轴于
,交x轴于![]() ,
, ![]() ,
,
根据对称性可知![]() ,
, ![]() ,
, ![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
![]() 直线
直线![]() 过点C,
过点C, ![]() 直线
直线![]() 解析式为
解析式为![]() ,
, ![]() 坐标为
坐标为![]() ,
,
综上所述,满足条件的点P坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
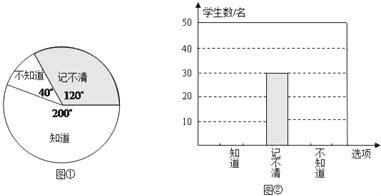
【题目】今年苏州市在全市中小学中开展以感恩和生命为主题的教育活动,各中小学结合学生实际,开展了形式多样的感恩教育活动.下面图①,图②分别是某校调查部分学生是否知道母亲生日情况的扇形统计图和条形统计图.根据图上信息,解答下列问题:
(1)求本次被调查学生的人数,并补全条形统计图;
(2)若全校共有2700名学生,你估计这所学校有多少名学生知道母亲的生日?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,粗线A→C→B和细线A→D→E→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.
(1)判断两条线路的长短;
(2)小丽坐出租车由体育馆B到少年宫A,假设出租车的收费标准为:起步价为7元,3千米以后每千米1.8元,用代数式表示出租车的收费m元与行驶路程s(s>3)千米之间的关系;
(3)如果这段路程长4.5千米,小丽身上有10元钱,够不够小丽坐出租车由体育馆到少年宫呢?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=4,AD=9点F是边BC上的一点,点E是AD上的一点,AE:ED=1:2,连接EF、DF,若EF=2![]() ,则CF的长为______________。
,则CF的长为______________。
查看答案和解析>>
科目:初中数学 来源: 题型:
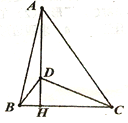
【题目】如图在△ABC中,AH⊥BC于点H,在AH上取一点D,连接DC,使DA=DC,且∠ADC=2∠DBC,若DH=2,BC=6,则AB=_________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P为抛物线y=x2+2x﹣3在第一象限内的一个动点,且P关于原点的对称点P′恰好也落在该抛物线上,则点P′的坐标为( )
A. (﹣1,﹣1) B. (﹣2,﹣![]() ) C. (﹣
) C. (﹣![]() ,﹣2
,﹣2![]() ﹣1) D. (﹣
﹣1) D. (﹣![]() ,﹣2
,﹣2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
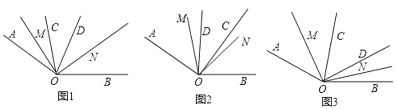
【题目】已知∠AOB=α(90°<α<180°),∠COD在∠AOB的内部,OM平分∠AOC,ON平分∠BOD.
(1)若∠COD=180°-α时,探索下面两个问题:
①如图1,当OC在OD左侧,求∠MON的度数;
②当OC在OD右侧,请在图2内补全图形,并求出∠MON的度数(用含α的代数式表示);
(2)如图3,当∠COD=kα,且CO在OD左侧时,直接写出∠MON的度数(用含α,k的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.
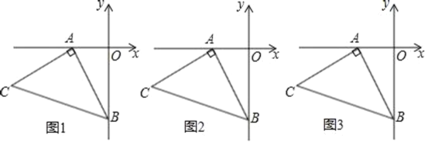
(1)求C点的坐标;
(2)如图1,在平面内是否存在一点H,使得以A、C、B、H为顶点的四边形为平行四边形?若存在,请直接写出H点坐标;若不存在,请说明理由;
(3)如图1点M(1,﹣1)是第四象限内的一点,在y轴上是否存在一点F,使得|FM﹣FC|的值最大?若存在,请求出F点坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将口ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com