
【题目】已知点P为抛物线y=x2+2x﹣3在第一象限内的一个动点,且P关于原点的对称点P′恰好也落在该抛物线上,则点P′的坐标为( )
A. (﹣1,﹣1) B. (﹣2,﹣![]() ) C. (﹣
) C. (﹣![]() ,﹣2
,﹣2![]() ﹣1) D. (﹣
﹣1) D. (﹣![]() ,﹣2
,﹣2![]() )
)
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.

(1)求证:四边形BDEF是平行四边形;
(2)线段BF、AB、AC的数量之间具有怎样的关系?证明你所得到的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
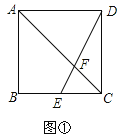
【题目】如图,点E是矩形ABCD的边BC的中点,连接DE交AC于点F.
![]() 如图
如图![]() ,求证:
,求证:![]() ;
;
![]() 如图
如图![]() ,作
,作![]() 于G,试探究:当AB与AD满足什么关系时,使得
于G,试探究:当AB与AD满足什么关系时,使得![]() 成立?并证明你的结论;
成立?并证明你的结论;
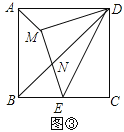
![]() 如图
如图![]() ,以DE为斜边在矩形ABCD内部作等腰
,以DE为斜边在矩形ABCD内部作等腰![]() ,交对角线BD于N,连接AM,若
,交对角线BD于N,连接AM,若![]() ,请直接写出
,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
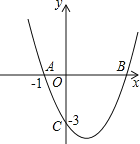
【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 两点,与x轴交于另一点B.
两点,与x轴交于另一点B.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 已知点
已知点![]() 在第四象限的抛物线上,求点D关于直线BC对称的点
在第四象限的抛物线上,求点D关于直线BC对称的点![]() 的坐标.
的坐标.
![]() 在
在![]() 的条件下,连接BD,问在x轴上是否存在点P,使
的条件下,连接BD,问在x轴上是否存在点P,使![]() ?若存在,请求出P点的坐标;若不存在,请说明理由.
?若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后解答问题(1)、(2)
解方程:|x+3|=2.
当x+30时,原方程可化为:x+3=2,解得x=1;
当x+3<0时,原方程可化为:x+3=2,解得x=5.
所以原方程的解是x=1,x=5.
(1)解方程:|3x1|5=0;
(2)探究:当b为何值时,方程|x2|=b+1①无解;②只有一个解;③有两个解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“一带一路”战略的影响下,某茶叶经销商准备把“茶路”融入“丝路”,经计算,他销售10kgA级别和20kgB级别茶叶的利润为4000元,销售20kgA级别和10kgB级别茶叶的利润为3500元.
(1)求每千克A级别茶叶和B级别茶叶的销售利润;
(2)若该经销商一次购进两种级别的茶叶共200kg用于出口,其中B级别茶叶的进货量不超过A级别茶叶的2倍,请你帮该经销商设计一种进货方案使销售总利润最大,并求出总利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
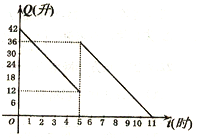
【题目】某机动车出发前油箱内有42升油,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图,回答下列问题(1)机动车行驶________小时后加油,中途加油_______升;(2)求加油前油箱剩余油量Q与行驶时间t的函数关系,并直接写出自变量t的取值范围;(3)如果加油站距目的地还有230千米,车速为40千米/时,要到达目的地,油箱中的油是否够用?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
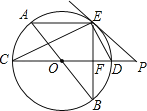
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com