
【题目】已知∠AOB=α(90°<α<180°),∠COD在∠AOB的内部,OM平分∠AOC,ON平分∠BOD.
(1)若∠COD=180°-α时,探索下面两个问题:
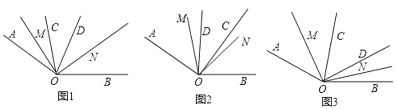
①如图1,当OC在OD左侧,求∠MON的度数;
②当OC在OD右侧,请在图2内补全图形,并求出∠MON的度数(用含α的代数式表示);
(2)如图3,当∠COD=kα,且CO在OD左侧时,直接写出∠MON的度数(用含α,k的代数式表示).
【答案】(1)①∠MON=90°;②∠MON=α90°;(2)∠MON的度数为![]() (1+k)α.理由见解析.
(1+k)α.理由见解析.
【解析】
(1)①根据角平分线的定义,得出∠AOM=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,再根据∠AOB=α,∠COD=180°α,得出∠AOC+∠BOD=∠AOB∠COD=α(180°α)=2α180°,进而得出∠AOM+∠BON=
∠BOD,再根据∠AOB=α,∠COD=180°α,得出∠AOC+∠BOD=∠AOB∠COD=α(180°α)=2α180°,进而得出∠AOM+∠BON=![]() (2α180°)=α90°,最后根据∠MON=∠AOB(∠AOM+∠BON)进行计算即可;②根据①中的方法进行计算,即可得出∠MON的度数;
(2α180°)=α90°,最后根据∠MON=∠AOB(∠AOM+∠BON)进行计算即可;②根据①中的方法进行计算,即可得出∠MON的度数;
(2)先根据角平分线的定义,得出∠AOM=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,再根据∠AOB=α,∠COD=kα,得出∠AOC+∠BOD=∠AOB∠COD=αkα,进而得到∠AOM+∠BON=
∠BOD,再根据∠AOB=α,∠COD=kα,得出∠AOC+∠BOD=∠AOB∠COD=αkα,进而得到∠AOM+∠BON=![]() (αkα)=
(αkα)=![]() α(1k),最后根据∠MON=∠AOB(∠AOM+∠BON)进行计算即可.
α(1k),最后根据∠MON=∠AOB(∠AOM+∠BON)进行计算即可.
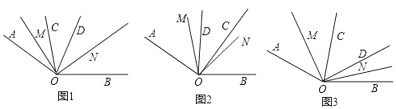
(1)①如图1,∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,
∠BOD,
∴∠AOM+∠BON=![]() (∠AOC+∠BOD),
(∠AOC+∠BOD),
∵∠AOB=α,∠COD=180°α,
∴∠AOC+∠BOD=∠AOB∠COD=α(180°α)=2α180°,
∴∠AOM+∠BON=![]() (2α180°)=α90°,
(2α180°)=α90°,
∴∠MON=∠AOB(∠AOM+∠BON)=α(α90°)=90°;
②当OC在OD右侧,补全图形如图2所画,
∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,
∠BOD,
∵∠AOB=α,∠COD=180°α,
∴∠AOC+∠BOD=∠AOB+∠COD=α+(180°α)=180°,
∴∠AOM+∠BON=![]() ×180°=90°,
×180°=90°,
∴∠MON=∠AOB(∠AOM+∠BON)=α90°;
(2)∠MON的度数为![]() (1+k)α.
(1+k)α.
理由:如图3,∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD,
∠BOD,
∴∠AOM+∠BON=![]() (∠AOC+∠BOD),
(∠AOC+∠BOD),
∵∠AOB=α,∠COD=kα,
∴∠AOC+∠BOD=∠AOB∠COD=αkα,
∴∠AOM+∠BON=![]() (αkα)=
(αkα)=![]() α(1k),
α(1k),
∴∠MON=∠AOB(∠AOM+∠BON)=α![]() α(1k)=
α(1k)=![]() (1+k)α.
(1+k)α.


科目:初中数学 来源: 题型:
【题目】某公司6天内货品进出仓库的吨数如下:(“+”表示进库,“-”表示出库)+31,-31,-16,+35,-38,-20
(1)经过这6天,仓库里的货品是______(填“增多了”或“减少了”)
(2)经过这6天,仓库管理员结算发现仓库还有货品460吨,那么6天前仓库里有货品多少吨?
(3)如果进出的装卸费都是每吨5元,那么这6天要付多少元装卸费?
查看答案和解析>>
科目:初中数学 来源: 题型:
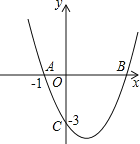
【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 两点,与x轴交于另一点B.
两点,与x轴交于另一点B.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 已知点
已知点![]() 在第四象限的抛物线上,求点D关于直线BC对称的点
在第四象限的抛物线上,求点D关于直线BC对称的点![]() 的坐标.
的坐标.
![]() 在
在![]() 的条件下,连接BD,问在x轴上是否存在点P,使
的条件下,连接BD,问在x轴上是否存在点P,使![]() ?若存在,请求出P点的坐标;若不存在,请说明理由.
?若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有![]() 三点分别表示数
三点分别表示数![]() ,且
,且![]() 满足
满足![]()
![]() .两只电子蚂蚁甲、乙分别从
.两只电子蚂蚁甲、乙分别从![]() 两点同时出发相向而行,若甲的速度为
两点同时出发相向而行,若甲的速度为![]() 个单位/秒,乙的速度为
个单位/秒,乙的速度为![]() 个单位/秒.
个单位/秒.
(1)求![]() 的值并在数轴上标出
的值并在数轴上标出![]() 三点.
三点.

(2)问甲、乙在数轴上的哪个点相遇?
(3)问多少秒后,甲到![]() 的距离为
的距离为![]() 个单位?
个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“一带一路”战略的影响下,某茶叶经销商准备把“茶路”融入“丝路”,经计算,他销售10kgA级别和20kgB级别茶叶的利润为4000元,销售20kgA级别和10kgB级别茶叶的利润为3500元.
(1)求每千克A级别茶叶和B级别茶叶的销售利润;
(2)若该经销商一次购进两种级别的茶叶共200kg用于出口,其中B级别茶叶的进货量不超过A级别茶叶的2倍,请你帮该经销商设计一种进货方案使销售总利润最大,并求出总利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
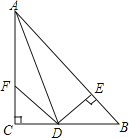
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF,BC=8,AB=10,则△FCD的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们知道,4x+2x-x=(4+2-1)x=5x,类似地,我们把(a+b)看成一个整体,则4(a+b)+2(a+b)-(a+b)-(4+2-1)(a+b)=5(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用:
(1)把(a-b)看成一个整体,合并3(a-b)2-7(a-b)2+2(a-b)2的结果是____________.
(2)已知x2-2y=5,求21-![]() x2+y的值;
x2+y的值;
(3)拓广探索:已知a-2b=3,2b-c=-5,c-d=10,求2(a-c)+2(2b-d)-2(2b-c)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
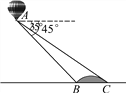
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.
(结果保留整数,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com