
【题目】如图,粗线A→C→B和细线A→D→E→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.
(1)判断两条线路的长短;
(2)小丽坐出租车由体育馆B到少年宫A,假设出租车的收费标准为:起步价为7元,3千米以后每千米1.8元,用代数式表示出租车的收费m元与行驶路程s(s>3)千米之间的关系;
(3)如果这段路程长4.5千米,小丽身上有10元钱,够不够小丽坐出租车由体育馆到少年宫呢?说明理由.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
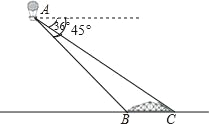
【题目】小明在热气球A上看到横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,36°.已知大桥BC与地面在同一水平面上,其长度为100m.请求出热气球离地面的高度(结果保留小数点后一位).参考数据:tan36°≈0.73.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司6天内货品进出仓库的吨数如下:(“+”表示进库,“-”表示出库)+31,-31,-16,+35,-38,-20
(1)经过这6天,仓库里的货品是______(填“增多了”或“减少了”)
(2)经过这6天,仓库管理员结算发现仓库还有货品460吨,那么6天前仓库里有货品多少吨?
(3)如果进出的装卸费都是每吨5元,那么这6天要付多少元装卸费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.(要求:用尺规作图,保留作图痕迹,不写作法,不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图1中ΔABC是等边三角形,DE是中位线,F是线段BC延长线上一点,且CF=AE,连接BE,EF.
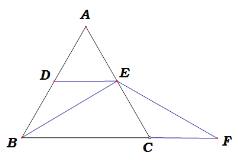
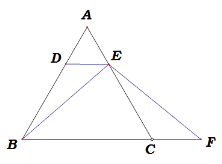
图1 图2
(1)求证:BE=EF;
(2)若将DE从中位线的位置向上平移,使点D、E分别在线段AB、AC上(点E与点A不重合),其他条件不变,如图2,则(1)题中的结论是否成立?若成立,请证明;若不成立.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
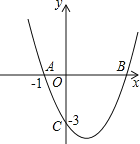
【题目】如图,抛物线![]() 经过
经过![]() 、
、![]() 两点,与x轴交于另一点B.
两点,与x轴交于另一点B.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 已知点
已知点![]() 在第四象限的抛物线上,求点D关于直线BC对称的点
在第四象限的抛物线上,求点D关于直线BC对称的点![]() 的坐标.
的坐标.
![]() 在
在![]() 的条件下,连接BD,问在x轴上是否存在点P,使
的条件下,连接BD,问在x轴上是否存在点P,使![]() ?若存在,请求出P点的坐标;若不存在,请说明理由.
?若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们知道,4x+2x-x=(4+2-1)x=5x,类似地,我们把(a+b)看成一个整体,则4(a+b)+2(a+b)-(a+b)-(4+2-1)(a+b)=5(a+b).“整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用:
(1)把(a-b)看成一个整体,合并3(a-b)2-7(a-b)2+2(a-b)2的结果是____________.
(2)已知x2-2y=5,求21-![]() x2+y的值;
x2+y的值;
(3)拓广探索:已知a-2b=3,2b-c=-5,c-d=10,求2(a-c)+2(2b-d)-2(2b-c)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com