
����Ŀ����ͼ��������ABCO�ı�OA��OC���������ϣ���B����Ϊ��6��6������������ABCO�Ƶ�C��ʱ����ת�ǶȦ���0�㣼����90�㣩���õ�������CDEF��ED���߶�AB�ڵ�G��ED���ӳ��߽��߶�OA�ڵ�H����CH��CG��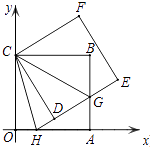
��1����֤����CBG�ա�CDG��
��2�����HCG�Ķ��������ж��߶�HG��OH��BG֮���������ϵ��˵�����ɣ�
��3������BD��DA��AE��EB�õ��ı���AEBD������ת�����У���G���ں�λ��ʱ�ı���AEBD�Ǿ��Σ���˵�����ɲ������H�����꣮
���𰸡�
��1��
֤�����߽�������ABCO�Ƶ�C��ʱ����ת�ǶȦ���
��DC=CO����CDG=��COA=90�㣬
���ı���OCBA�������Σ�
��CB=CO����B=90�㣬
��CB=CD����B=��CDG=90��
��Rt��CDG��Rt��CBG��
![]() ��
��
��Rt��CDG��Rt��CBG
��2��
�⣺�ߡ�CDG=90�㣬
���CDH=90�㣬
��Rt��COH��Rt��CDH��
![]() ��
��
��Rt��COH��Rt��CDH��
���OCH=��DCH��HO=DH��
��Rt��CDG��Rt��CBG��
���DCG=��BCG��DG=BG��
���HCG=��DCG+��DCH=45�㣬
HG=HD+DG=HO+BG
��3��
�⣺��G��AB�е�ʱ���ı���ADBE�Ǿ��Σ�
��G��AB�е㣬
��BG=AG= ![]() AB
AB
�ɣ�2����DG=BG��
�֡�AB=DE��
��DG= ![]() DE��
DE��
��DG=GE=BG=AG��
���ı���AEBD��ƽ���ı��Σ�
��AB=DE��
���ADBE�Ǿ��Σ�
���H��������x��0����
��HO=HD=x��DG=BG=AG=3��AH=6��x��
�ɹ��ɶ����ã���6��x��2+33=��3+x��2��
��ã�x=2��
��H��2��0����
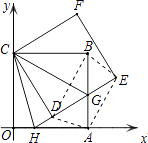
����������1��������ת�任�����ʵõ�DC=CO����CDG=��COA=90�㣬���������ε����ʵõ�CB=CO����B=90�㣬����ֱ�������ε�ȫ�ȵ��ж�����֤�����ɣ���2��֤��Rt��COH��Rt��CDH���õ���OCH=��DCH��HO=DH�������������ɣ���3�����ݾ��ε��ж�����֤���ı���AEBD�Ǿ��Σ����H������Ϊ��x��0�������ݹ��ɶ����г����̣��ⷽ�����x��ֵ���õ���H�����꣮


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ�����ҵı�����ȷ����( )
A. -x-y=-(x-y) B. -x2+2xy-y2=-(x2+2xy+y2)
C. (y-x)2=(x-y)2 D. (y-x)3=(x-y)3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˰��涨�ļ�������ij��ҩ���÷�ҩ��2Сʱ��ÿ����ѪҺ�еĺ�ҩ���ﵽ���ֵΪ4���ˣ���֪��ҩ��2Сʱǰÿ����ѪҺ�еĺ�ҩ��y�����ˣ���ʱ��x��Сʱ������������2Сʱ��y��x�ɷ���������ͼ��ʾ��������������Ϣ����������⣮ 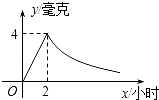
��1����y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����ÿ����ѪҺ�еĺ�ҩ��������2����ʱ������Ч����ô���˷�ҩһ�����Ƽ�������Чʱ���Ƕ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=�� ![]() ��ͼ���һ�κ���y=kx��1��ͼ������P��m����3m����
��ͼ���һ�κ���y=kx��1��ͼ������P��m����3m���� 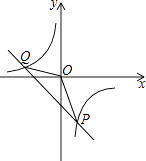
��1�����P����������һ�κ����ı���ʽ��
��2����������ͼ�����һ������Q������Ϊ2��OΪ����ԭ�㣬���POQ�������
��3������M��a��y1���͵�N��a+1��y2���������������������ͼ���ϣ��Ƚ�y1��y2�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���A=75�㣬��B=50�㣬����ABC�Ƶ�C����ʱ�뷽����ת���õ���A��B��C����A�Ķ�Ӧ��A������AB���ϣ����BCA'�Ķ���Ϊ�� �� 
A.20��
B.25��
C.30��
D.35��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��2����3���ڷ���������y= ![]() ��ͼ���ϣ�
��ͼ���ϣ�
��1�����жϵ�B����1��6����C����3����2���Ƿ������������������ͼ���ϣ���˵�����ɣ�
��2����P��a��1��b����Q��a��c��Ҳ�����������������ͼ���ϣ���a��0���ԱȽ�b��c�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��AD��BC��D�㣬E��F�ֱ�ΪDB��DC���е㣬��ͼ�й���ȫ���������ԣ� 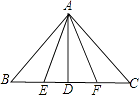
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com