练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知抛物线y=ax2+bx+c经过点A（0，3）、B（4，3）、C（1，0）、
    （1）填空：抛物线的对称轴为直线x= ， 抛物线与x轴的另一个交点D的坐标为；
    （2）求该抛物线的解析式．

    【答案】
    （1）2；（3，0）
    （2）解：∵拋物线经过点C（1，0）、D（3，0），

    ∴设拋物线的解析式为y=a（x﹣1）（x﹣3）

    由拋物线经过点A（0，3），得a=1

    ∴拋物线的解析式为y=x2﹣4x+3


    【解析】解：（1）拋物线的对称轴为直线x=2；
    拋物线与x轴的另一个交点D的坐标为（3，0）；
    【考点精析】通过灵活运用二次函数的性质，掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，若BC=EC，∠BCE=∠ACD，则添加不能使△ABC≌△DBC的条件是（ ）

    A．AB=DE B．∠B=∠E C．AC=DC D．∠A=∠D

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将在Rt△ABC绕其锐角顶点A旋转90°得到在Rt△ADE，连接BE，延长DE、BC相交于点F，则有∠BFE=90°，且四边形ACFD是一个正方形．

    （1）判断△ABE的形状，并证明你的结论；

    （2）用含b代数式表示四边形ABFE的面积；

    （3）求证：a2+b2=c2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市某县政府为了迎接“八一”建军节，加强军民共建活动，计划从花园里拿出1430盆甲种花卉和1220盆乙种花卉，搭配成A、B两种园艺造型共20个，在城区内摆放，以增加节日气氛，已知搭配A、B两种园艺造型各需甲、乙两种花卉数如表所示：（单位：盆）

    （1）某校某年级一班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮忙设计出来．

    （2）如果搭配及摆放一个A造型需要的人力是8人次，搭配及摆放一个B造型需要的人力是11人次，哪种方案使用人力的总人次数最少，请说明理由．

    造型数量花

    A

    B

    甲种

    80

    50

    乙种

    40

    90

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】纸箱厂用如图1所示的长方形和正方形纸板，做成如图2所示的竖式与横式两种长方体形状的有底无盖纸盒．

    （1）现有正方形纸板172张，长方形纸板330张．若要做两种纸盒共l00个，设做竖式纸盒x个．

    ①根据题意，完成以下表格：

    纸盒
    纸板

    竖式纸盒(个)

    横式纸盒(个)

    x


    正方形纸板(张)


    2(100-x)

    长方形纸板(张)

    4x


    ②按两种纸盒的数量分，有哪几种生产方案?

    （2）若有正方形纸板112张，长方形纸板张，做成上述两种纸盒，纸板恰好用完．已知100<<110，则的值是 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解一元二次不等式 ．

    请按照下面的步骤，完成本题的解答．

    解： 可化为 ．

    （1）依据“两数相乘，同号得正”，可得不等式组① 或不等式组②________．

    （2）解不等式组①，得________．

    （3）解不等式组②，得________．

    （4）一元二次不等式 的解集为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠B=60°，∠C=20°，AD为△ABC的高，AE为角平分线．求∠EAD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=﹣x2+bx+c与x轴交于点A（1，0），B（3，0），与y轴交于点C．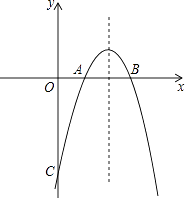
    （1）求抛物线的解析式；
    （2）设点P在该抛物线上滑动，则满足S△PAB=1的点P有几个？求出所有点P的坐标；
    （3）在该抛物线的对称轴上存在点M，使得△MAC的周长最小，求出这个点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y=ax2+bx+c的图象与x轴交于（﹣2，0）和（4，0）两点，当函数值y＞0时，自变量x的取值范围是（ ）
    A.x＜﹣2
    B.x＞4
    C.﹣2＜x＜4
    D.x＞0

    查看答案和解析>>

    同步练习册答案