练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，△ABC中，AB=AC，BD=CF，BE=CD，∠EDF=a，则下列结论正确的是（　　）

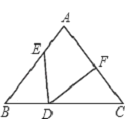
    A. a+∠A=90° B. a+∠A=180° C. 2a+∠A=90° D. 2a+∠A=180°

    【答案】D

    【解析】

    根据已知条件可证明△BDE≌△CFD，则∠BED=∠CDF，由∠A+∠B+∠C=180°，得∠B=，因为∠BDE+∠EDF+∠CDF=180°，所以得出a与∠A的关系．

    解：在△BDE和△CFD中，，

    ∴△BDE≌△CFD，

    ∴∠BED=∠CDF，

    ∵∠A+∠B+∠C=180°，

    ∴∠B=，

    ∵∠BDE+∠EDF+∠CDF=180°，

    ∴180°-∠B-∠BED+a+∠CDF=180°，

    ∴∠B=a，

    即=a，

    整理得2a+∠A=180°．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，（M2，N2），∠BAC=30°，E为AB边的中点，以BE为边作等边△BDE，连接AD，CD．

    （1）求证：△ADE≌△CDB；

    （2）若BC=，在AC边上找一点H，使得BH+EH最小，并求出这个最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直径为10cm的⊙O中，弦AB的长为5 cm，则AB所对的圆周角是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

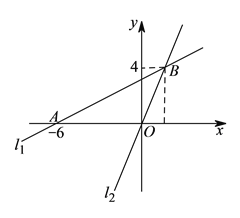
    【题目】如图，在平面直角坐标系中，过点的直线与直线；相交于点．

    （）求直线的表达式．

    （）过动点且垂于轴的直线与、的交点分别为，，当点位于点上方时，写出的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

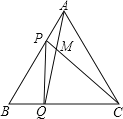
    【题目】点P、Q分别是边长为4cm的等边的边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都是，设运动时间为t秒．

    连接AQ、CP交于点M，则在P、Q运动的过程中，变化吗：若变化，则说明理由，若不变，则求出它的度数；

    连接PQ，

    当秒时，判断的形状，并说明理由；

    当时，则______秒直接写出结果

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在Rt△ABC中，∠C=90°，BC=6cm,AC=8 cm，AB=10 cm. 现有一动点P，从A点出发，沿着三角形的边AC-CB-BA运动，回到A点停止，速度为1 cm/s，设运动时间为t s.

    （1）当t=_______时，△ABC的周长被线段AP平分为相等的两部分.

    （2）当t=_______时，△APC的面积等于△ABC面积的一半.

    （3）还有一个△DEF，∠E=90°，如图②所示，DE=4cm，DF=5cm，∠D=∠A. 在△ABC的边上，若另外有一个动点Q，与P 同时从A点出发，沿着边AB-BC-CA运动，回到点A停止. 在两点运动过程中某一时刻，恰好△APQ与△DEF全等，则点Q的运动速度 cm/s.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题中，正确的有（ ）

    ①Rt△ABC中，已知两边长分别为3和4，则第三边长为5；

    ②有一个内角等于其他两个内角和的三角形是直角三角形；

    ③三角形的三边分别为a，b，C，若a2+c2=b2，那么∠C=90°；

    ④若△ABC中，∠A：∠B：∠C=1：5：6，则△ABC是直角三角形．

    A．1个 B．2个 C．3个 D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

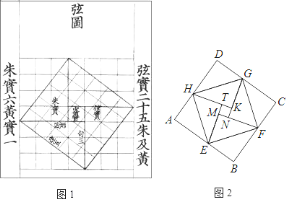
    【题目】我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图），图由弦图变化得到，它是由作个全等的直角三角形拼接而成，记图中正方形，正方形，正方形的面积分别为、、，若，则的值是（ ）

    A. 5 B. C. D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一次函数y=x+m（m≠0）与反比例函数 的图象在同一平面直角坐标系中是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案