
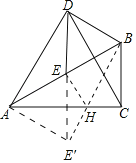
【题目】如图,在Rt△ABC中,(M2,N2),∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.
(1)求证:△ADE≌△CDB;
(2)若BC=![]() ,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.

【答案】(1)证明见解析;(2)BH+EH的最小值为3.
【解析】
(1)只要证明△DEB是等边三角形,再根据SAS即可证明;
(2)如图,作点E关于直线AC点E',连接BE'交AC于点H.则点H即为符合条件的点.
(1)在Rt△ABC中,∠BAC=30°,E为AB边的中点,
∴BC=EA,∠ABC=60°,
∵△DEB为等边三角形,
∴DB=DE,∠DEB=∠DBE=60°,
∴∠DEA=120°,∠DBC=120°,
∴∠DEA=∠DBC,
∴△ADE≌△CDB;
(2)如图,作点E关于直线AC点E',连接BE'交AC于点H,则点H即为符合条件的点,
由作图可知:EH=HE',AE'=AE,∠E'AC=∠BAC=30°,
∴∠EAE'=60°,
∴△EAE'为等边三角形,
∴E E'=EA=![]() AB,
AB,
∴∠AE'B=90°,
在Rt△ABC中,∠BAC=30°,BC=![]() ,
,
∴AB=2![]() ,A E'=AE=
,A E'=AE=![]() ,
,
∴B E'=![]() =3,
=3,
∴BH+EH的最小值为3.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( ) 
A.![]()
B.6
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
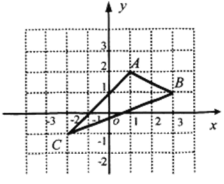
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
⑴.在图中作出△ABC关于y轴对称的△A1B1C1.
⑵.写出点A1,B1,C1的坐标(直接写出答案).
A1 B1 C1 ;
⑶.△A1B1C1的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了丰富学生的校园体育锻炼生活,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用,因此学校随机抽取了部分同学就兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题: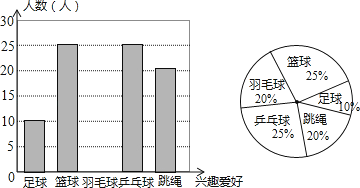
(1)设学校这次调查共抽取了n名学生,直接写出n的值;
(2)请你补全条形统计图;
(3)设该校共有学生1200名,请你估计该校有多少名学生喜欢跳绳?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一列按一定顺序和规律排列的数:
第一个数是 ![]() ;
;
第二个数是 ![]() ;
;
第三个数是 ![]() ;
;
…
对任何正整数n,第n个数与第(n+1)个数的和等于 ![]() .
.
(1)经过探究,我们发现: ![]()
设这列数的第5个数为a,那么 ![]() ,
, ![]() ,
, ![]() ,哪个正确?
,哪个正确?
请你直接写出正确的结论;
(2)请你观察第1个数、第2个数、第3个数,猜想这列数的第n个数(即用正整数n表示第n数),并且证明你的猜想满足“第n个数与第(n+1)个数的和等于 ![]() ”;
”;
(3)设M表示 ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,这2016个数的和,即
,这2016个数的和,即 ![]() ,
,
求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至G,取NG=NQ,若△MNP的周长为12,MQ=a,则△MGQ周长是( )
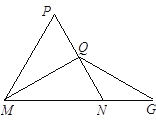
A. 8+2a B. 8+a C. 6+a D. 6+2a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,则S2的值是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b,那么(a+b)2的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,BD=CF,BE=CD,∠EDF=a,则下列结论正确的是( )
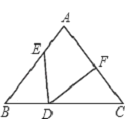
A. a+∠A=90° B. a+∠A=180° C. 2a+∠A=90° D. 2a+∠A=180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com