
【题目】已知:四边形ABCD是正方形,E是AB边上一点,F是BC延长线上一点,且DE=DF.
(1)如图1,求证:DF⊥DE; 
(2)如图2,连接AC,EF交于点M,求证:M是EF的中点. 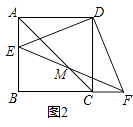
【答案】
(1)证明:∵四边形ABCD是正方形,
∴DA=DC,∠DAE=∠DCB=90°.
∴∠DCF=180°﹣90°=90°.
∴∠DAE=∠DCF.
在Rt△DAE和Rt△DCF中, ![]() ,
,
∴Rt△DAE≌Rt△DCF(HL).
∴∠ADE=∠CDF,
∵∠ADE+∠CDE=90°,
∴∠CDF+∠CDE=90°,
即∠EDF=90°,
∴DF⊥DE.
(2)证明;过点F作GF⊥CF交AC的延长线于点G,
则∠GFC=90°.
∵正方形ABCD中,∠B=90°,
∴∠GFC=∠B.
∴AB∥GF.
∴∠BAC=∠G.
∵四边形ABCD是正方形,
∴AB=BC,
∴∠BAC=∠BCA=45°.
∴∠BAC=∠BCA=∠FCG=∠G=45°.
∴FC=FG.
∵△DAE≌△DCF,
∴AE=CF.
∴AE=FG.
在△AEM和△GFM中, 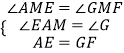 ,
,
∴△AEM≌△GFM(AAS).
∴ME=MF.
即M是EF的中点
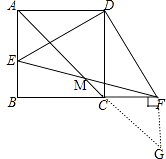
【解析】(1)由正方形的性质得出DA=DC,∠DAE=∠DCB=90°.得出∠DAE=∠DCF.由HL证明Rt△DAE≌Rt△DCF,得出∠ADE=∠CDF,证出∠EDF=90°即可;(2)证明;过点F作GF⊥CF交AC的延长线于点G,则∠GFC=90°.AB∥GF.得出∠BAC=∠G.由正方形的性质证出FC=FG.得出AE=FG.由AAS证明△AEM≌△GFM,得出ME=MF即可.


科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM、射线AE于点F、D.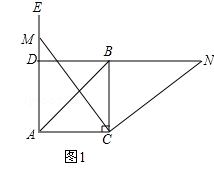
(1)直接写出∠NDE的度数.
(2)如图2、图3,当∠EAC为锐角或钝角时,其他条件不变,(1)中的结论是否发生变化?如果不变,选取其中一种情况加以证明;如果变化,请说明理由.

(3)如图4,若∠EAC=15°,∠ACM=60°,直线CM与AB交于G,BD=![]() ,其他条件不变,求线段AM的长.
,其他条件不变,求线段AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过 点A,C 画一条射线AE,AE就是∠PRQ的平分线。此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE。则说明这两个三角形全等的依据是( )

A. SSS B. SAS C. ASA D. AAS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、E、F、D四点在同一直线上,CE∥BF,CE=BF,∠B=∠C.(1)△ABF与△DCE全等吗?请说明理由;(2)AB与CD平行吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国汉字听写大会”是由中央电视台和国家语言文学工作委员会联合主办的节目,希望通过节目的播出,能吸引更多的人关注对汉字文化的学习,某校开展了一次“汉字听写”比赛,每位参赛学生听写40个汉字,比赛结束后随机抽取部分学生的听写结果,按听写正确的汉字个数x绘制成了如图两幅不完整的统计图.
根据以上信息回答下列问题:
(1)本次共随机抽取了名学生的听写结果,听写正确的汉字个数x在范围的人数最多;
(2)补全频数分布直方图;
(3)在扇形统计图中,请计算31≤x≤41所对应的扇形圆心角的大小;
(4)若该校共有1200名学生,如果听写正确的汉字个数不少于21个定为良好,请你估计该校本次“汉字听写”比赛达到良好的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=1,连接AC,以AC为边作第一个正方形ACC1D1 , 连接AC1 , 以AC1为边作第二个正方形AC1C2D2 , 则第10个正方形边长为( ) 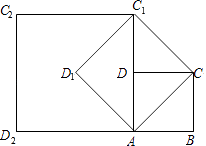
A.8
B.16
C.32
D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。

(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制成图表时发现,优秀漏统计![]() 人,良好漏统计
人,良好漏统计![]() 人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
(1)填写统计表.
(2)根据调整后数据,补全条形统计图.
(3)若该校共有学生![]() 人,请你估算出该校体能测试等级为“优秀”的人数.
人,请你估算出该校体能测试等级为“优秀”的人数.
学生体能测试成绩各等次人数统计表
体能等级 | 调整前人数 | 调整后人数 |
优秀 |
| |
良好 |
| |
及格 |
| |
不及格 |
| |
合计 |
|
学生体能测试成绩各等次人数统计图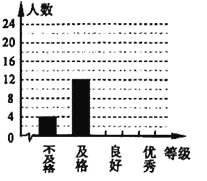
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com