
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣1,且抛物线经过 A(1,0),C(0,3)两点,与x轴交于点B.
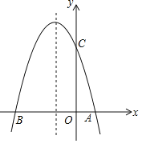
(1)求抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求此时点M的坐标;
(3)设点P为抛物线对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
【答案】(1)y=﹣x2﹣2x+3;(2)当点M的坐标为(﹣1,2)时,点M到点A和点C的距离之和最小;(3)P(﹣1,﹣2)或(﹣1,4)或(﹣1,![]()
![]() )或(﹣1,
)或(﹣1,![]() ).
).
【解析】
(1)根据对称轴公式及A、C两点坐标代入即可求出抛物线的解析式;
(2)根据两条线段之和最短时的作图方法找到M即可,然后利用B、C的坐标求出直线BC的解析式,利用BC和对称轴即可求出M的坐标;
(3)设P(﹣1,t),根据平面直角坐标系中任意两点之间的距离公式,即可表示出CB2,PB2和PC2,然后根据直角顶点分类讨论,利用勾股定理求t即可.
解:(1)根据题意得: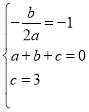 ,解得:
,解得: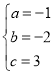 ,
,
∴抛物线的解析式为:y=﹣x2﹣2x+3.
(2)点A的对称点为B,连接BC,直线BC与对称轴x=﹣1的交点为M,则此时AM+MC的值最小.
∵点A与点B关于x=﹣1对称,A(1,0),
∴B(﹣3,0).
设BC的解析式为y=mx+n,将点B和点C的坐标代入得:![]() ,解得:m=1,n=3.
,解得:m=1,n=3.
∴直线BC的解析式为y=x+3.
将x=﹣1代入y=x+3得:y=2,
∴M(﹣1,2).
∴当点M的坐标为(﹣1,2)时,点M到点A和点C的距离之和最小.
(3)设P(﹣1,t).
∵P(﹣1,t),B(﹣3,0),C(0,3),
∴CB2=18,PB2=(﹣1+3)2+t2=t2+4,PC2=(﹣1)2+(t﹣3)2=t2﹣6t+10.
①当点B为直角顶点时,则BC2+PB2=PC2,即18+t2+4=t2﹣6t+10,解得t=﹣2,
∴P(﹣1,﹣2).
②当点C为直角顶点时,BC2+PC2=PB2,即18+t2﹣6t+10=t2+4,解得t=4,
∴P(﹣1,4).
③当点P为直角顶点时,PC2+PB2=BC2,即t2+4+t2﹣6t+10=18,解得:t=![]() 或t=
或t=![]() ,
,
∴P(﹣1,![]() )或(﹣1,
)或(﹣1,![]() ).
).
综上所述,点P的坐标为P(﹣1,﹣2)或(﹣1,4)或(﹣1,![]() )或(﹣1,
)或(﹣1,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,顶点为点
,顶点为点![]() .
.
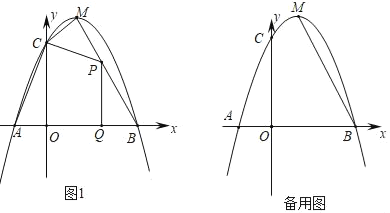
(1)求这条抛物线的解析式及直线![]() 的解析式;
的解析式;
(2)![]() 段
段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 向
向![]() 轴引垂线,垂足为
轴引垂线,垂足为![]() ,设
,设![]() 的长为
的长为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() .求
.求![]() 与
与![]() 之间的函数关系式及自变量
之间的函数关系式及自变量![]() 的取值范围;
的取值范围;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出点
为等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实国务院房地产调控政策,使“居者有其屋”.某市加快了廉租房的建设力度,2013年市政府共投资3亿元人民币建设了廉租房12万平方米,2015年投资6.75亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,问2015年建设了多少万平方米廉租房?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、P、B为⊙O上的三点,
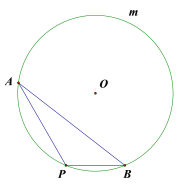
(1)在优弧AmB上求作一点C,使得![]() (尺规作图,保留作图痕迹,不写作法);
(尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,若∠APB=120°,连接AC,BC,求证:△ABC是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数图象如图所示,根据图象可得:
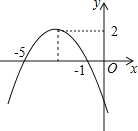
(1)抛物线顶点坐标_____.
(2)对称轴为_____.
(3)当_____时,y随着x得增大而增大
(4)当_____时,y>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且经
,且经![]() 、
、![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在抛物线的对称轴
在抛物线的对称轴![]() 上,是否存在点
上,是否存在点![]() ,使它到点
,使它到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,如果存在求出点
的距离之和最小,如果存在求出点![]() 的坐标,如果不存在请说明理由.
的坐标,如果不存在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
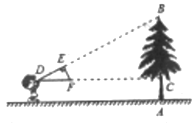
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形![]() 中,G、H分别是
中,G、H分别是![]() 、
、![]() 的中点,E、O、F分别是对角线
的中点,E、O、F分别是对角线![]() 上的四等分点,顺次连接G、E、H、F.
上的四等分点,顺次连接G、E、H、F.
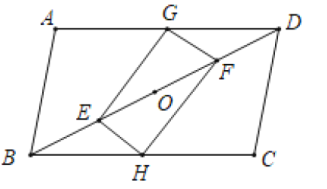
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当平行四边形![]() 满足_______条件时,四边形
满足_______条件时,四边形![]() 是菱形;
是菱形;
(3)若![]() ,探究四边形
,探究四边形![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
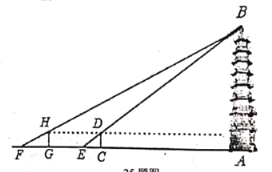
【题目】净觉寺享有“家东第一寺”的美誉,是一座规模较大,布局严颜,结构合理,独具一格的古建筑群体,被国务院批准列入第六批全国重点文物保护单位名单,某校社会实践小组为了测量寺内一古塔的高度,在地面上![]() 处垂直于地面竖立了高度为
处垂直于地面竖立了高度为![]() 米的标杆
米的标杆![]() ,这时地面上的点
,这时地面上的点![]() ,标杆的顶端点
,标杆的顶端点![]() ,古塔的塔尖点
,古塔的塔尖点![]() 正好在同一直线上,测得
正好在同一直线上,测得![]() 米,将标杆向后平移到点处,这时地面上的点
米,将标杆向后平移到点处,这时地面上的点![]() ,标杆的顶端点
,标杆的顶端点![]() ,古塔的塔尖点
,古塔的塔尖点![]() 正好在同一直线上(点
正好在同一直线上(点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 与古塔底处的点
与古塔底处的点![]() 在同一直线上)这时测得
在同一直线上)这时测得![]() 米,
米,![]() 米,请你根据以上数据,计算古塔的高度
米,请你根据以上数据,计算古塔的高度![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com