
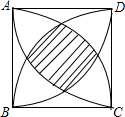
 如图,正方形ABCD的边长为a,分别以正方形的四个顶点为圆心,边长为半径,在正方形内画弧,求图中阴影部分的面积.
如图,正方形ABCD的边长为a,分别以正方形的四个顶点为圆心,边长为半径,在正方形内画弧,求图中阴影部分的面积. 分析 如图所示,设图中各部分面积分别为x,y,z,由题意可知图中三角形为等边三角形,利用扇形的面积,三角形面积公式,正方形面积公式可得关于x,y,z的方程组,解得z即为所求阴影部分的面积.
解答 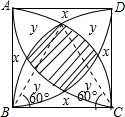 解:如图所示,设图中各部分面积分别为x,y,z,
解:如图所示,设图中各部分面积分别为x,y,z,
由题意得:4x+4y+z=a2 ①,
2x+y=a2-$\frac{π}{4}a$2 ②,
3x+2y=a2-(2•$\frac{π}{6}$a2-$\frac{1}{2}$×$\frac{\sqrt{3}}{2}a$×a) ③,
③-②得,x+y=$\frac{3\sqrt{3}-π}{12}$a2 ④,
将④代入①得z=$\frac{3+π-3\sqrt{3}}{3}$a2.
点评 本题主要考查了等边三角形和扇形的面积及不规则图形面积的计算,数形结合,利用规则图形的面积计算不规则图形的面积是解答此题的关键.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:选择题
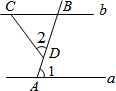 如图,已知:直线a、b被AB所截,交点分别是点A、B,其中a∥b,∠1=72°,点D是线段AB上一点,CD=BD.则∠2=( )
如图,已知:直线a、b被AB所截,交点分别是点A、B,其中a∥b,∠1=72°,点D是线段AB上一点,CD=BD.则∠2=( )| A. | 72° | B. | 36° | C. | 64° | D. | 56° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>0,b2-4ac≥0 | B. | a<0,b2-4ac≥0 | C. | a>0,b2-4ac<0 | D. | a<0,b2-4ac<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com