
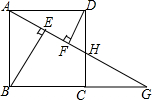
 如图,四边形ABCD是正方形,G是BC的延长线上一点,连接AG交CD于点H,BE⊥AG于点E,DF⊥AG于点F.
如图,四边形ABCD是正方形,G是BC的延长线上一点,连接AG交CD于点H,BE⊥AG于点E,DF⊥AG于点F.分析 (1)由正方形的性质得出AB=AD,∠BAD=90°,由角的关系得出∠ABE=∠DAF,由AAS证明△ABE≌△DAF即可;
(2)由含30°角的Rt△BEG得出BE=$\frac{1}{2}$BG=2$\sqrt{3}$,再求出∠ABE=30°,则Rt△ABE得出AB=2AE,设AE=x,则AB=2x,由勾股定理得:x2+(2$\sqrt{3}$)2=(2x)2,
解得x=2,由△ABE≌△DAF,得出AF=BE=2$\sqrt{3}$,即可求出结果;
(3)由H为CD的中点,得出CH=DH=$\frac{1}{2}$AB=$\frac{1}{2}$AD=$\frac{1}{2}$CD,由AAS证得△ADH≌△CGH得出HG=AH,CG=AD,tan∠HGC=$\frac{HC}{CG}$=$\frac{HC}{AD}$=$\frac{1}{2}$,证得AF=2DF,由△ABE≌△DAF得出AE=EF=DF,再由∠HDF=∠DAF得出DF=2FH,即可得出结果.
解答 (1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵BE⊥AG,DF⊥AG,
∴∠BEA=∠AFD=90°,
∴∠BAE+∠ABE=90°,
∵∠BAE+∠DAF=90°,
∴∠ABE=∠DAF,
在△ABE和△DAF中,$\left\{\begin{array}{l}{∠ABE=∠DAF}\\{∠BEA=∠AFD}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△DAF(AAS);
(2)解:在Rt△BEG中,∠AGB=30°,BG=4$\sqrt{3}$,
∴BE=$\frac{1}{2}$BG=2$\sqrt{3}$,
∵∠GBE=90°-∠BGE=60°,
∴∠ABE=30°,
∴AB=2AE,
设AE=x,则AB=2x,
在Rt△ABE中,由勾股定理得:x2+(2$\sqrt{3}$)2=(2x)2,
解得:x=2,
∴AE=2,
∵△ABE≌△DAF,
∴AF=BE=2$\sqrt{3}$,
∴EF=AF-AE=2$\sqrt{3}$-2;
(3)解:EH=$\frac{3}{5}$HG,理由如下:
∵H为CD的中点,
∴CH=DH=$\frac{1}{2}$AB=$\frac{1}{2}$AD=$\frac{1}{2}$CD,
∵四边形ABCD是正方形,
∴AD∥BG,
∴∠HGC=∠DAF,
在△ADH和△CGH中,$\left\{\begin{array}{l}{∠HGC=∠DAF}\\{∠HCG=∠HDA=90°}\\{CH=DH}\end{array}\right.$,
∴△ADH≌△CGH(AAS),
∴HG=AH,CG=AD,tan∠HGC=$\frac{HC}{CG}$=$\frac{HC}{AD}$=$\frac{1}{2}$,
∵∠HGC=∠DAF,
∴AF=2DF,
∵△ABE≌△DAF,
∴AF=AB,AE=DF,
∴AE=EF=DF,
∵∠HDF=∠DAF,
∴DF=2FH,
∴AH=5FH,EH=$\frac{3}{5}$AH,
即EH=$\frac{3}{5}$HG.
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质、勾股定理等知识;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,菱形ABCD中,∠A=60°,边长为4厘米,动点P从A出发,以1厘米/秒的速度沿A-B-C运动,在P出发1秒后,点Q以同样的速度沿相同的路线运动,过点P、Q的直线L1、L2相互平行,且都与AB边所在的直线成60°角,设P点运动的时间为x秒(1<x<8),直线L1、L2在菱形ABCD上截得的图形面积为y平方厘米.
如图,菱形ABCD中,∠A=60°,边长为4厘米,动点P从A出发,以1厘米/秒的速度沿A-B-C运动,在P出发1秒后,点Q以同样的速度沿相同的路线运动,过点P、Q的直线L1、L2相互平行,且都与AB边所在的直线成60°角,设P点运动的时间为x秒(1<x<8),直线L1、L2在菱形ABCD上截得的图形面积为y平方厘米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等腰梯形ABCD中,AD∥BC,AB=5,AD=9,tanB=$\frac{4}{3}$,P是BC上的动点(与B、C不重合),作∠APQ=∠B,PQ交射线AD于点Q,设BP=x,QD=y
如图,等腰梯形ABCD中,AD∥BC,AB=5,AD=9,tanB=$\frac{4}{3}$,P是BC上的动点(与B、C不重合),作∠APQ=∠B,PQ交射线AD于点Q,设BP=x,QD=y查看答案和解析>>
科目:初中数学 来源: 题型:选择题
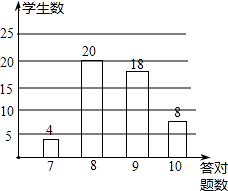 数学老师布置10道选择欢迎登陆全品中考网“题作为课堂练习,学习委员将全班同学的答欢迎登陆全品中考网“题情况绘制成条形图(图在第一面),根据统计图可知,答对8道欢迎登陆全品中考网“题的同学的频率是( )
数学老师布置10道选择欢迎登陆全品中考网“题作为课堂练习,学习委员将全班同学的答欢迎登陆全品中考网“题情况绘制成条形图(图在第一面),根据统计图可知,答对8道欢迎登陆全品中考网“题的同学的频率是( )| A. | 0.38 | B. | 0.4 | C. | 0.16 | D. | 0.08 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
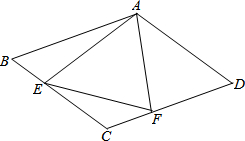 如图所示,在菱形ABCD中,AB=8cm,∠BAD=120°,点E、F分别是边BC、CD上的两个动点,E点从点B向点C运动,F点从点D向点C运动,设点E、F运动的路径长分别是acm和bcm.
如图所示,在菱形ABCD中,AB=8cm,∠BAD=120°,点E、F分别是边BC、CD上的两个动点,E点从点B向点C运动,F点从点D向点C运动,设点E、F运动的路径长分别是acm和bcm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com