
 如图,等腰梯形ABCD中,AD∥BC,AB=5,AD=9,tanB=$\frac{4}{3}$,P是BC上的动点(与B、C不重合),作∠APQ=∠B,PQ交射线AD于点Q,设BP=x,QD=y
如图,等腰梯形ABCD中,AD∥BC,AB=5,AD=9,tanB=$\frac{4}{3}$,P是BC上的动点(与B、C不重合),作∠APQ=∠B,PQ交射线AD于点Q,设BP=x,QD=y分析 (1)过A作AH⊥BC于点H,可以求出AH,BH的长度,然后在Rt△AHP中,利用勾股定理表示AP的长度;
(2)根据等腰梯形的性质求出AD、BC的长度,然后证明△APQ和△PBA相似,根据相似三角形对应边成比例的性质列出比例式,再代入数据进行整理即可得到y关于x的函数解析式;
(3)①如果DQ=CD=5,过C作CG⊥DQ于G,如图2,解直角三角形得到DG=AH=4,DG=3,根据勾股定理即可得到结论;②如果CQ=CD,得到CQ=5,③如果DQ=CQ,过Q作QL⊥CD于L,如图3,根据等腰三角形的性质得到DL=CL=$\frac{5}{2}$,根据三角函数的定义得到QL=$\frac{10}{3}$,根据勾股定理得到CQ=$\sqrt{C{L}^{2}+L{Q}^{2}}$=$\frac{25}{6}$.
解答 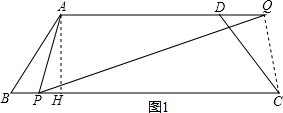 解:(1)如图1,作AH⊥BC于点H.
解:(1)如图1,作AH⊥BC于点H.
∵tanB=$\frac{4}{3}$,AB=5,
∴BH=3,AH=4,
在Rt△AHP中,
AP=$\sqrt{(3-x)^{2}+{4}^{2}}$=$\sqrt{{x}^{2}-6x+25}$;
(2)∵AD=9,
∴BC=6+9=15,
∵AD∥BC,
∴∠PAQ=∠APB,
∵∠APQ=∠B.
∴△APQ∽△PBA,
∴$\frac{AQ}{AP}$=$\frac{AP}{BP}$,
∴$\frac{y+4}{\sqrt{{x}^{2}-6x+25}}$=$\frac{\sqrt{{x}^{2}-6x+25}}{x}$.
∴y=$\frac{{x}^{2}-10x+25}{x}$ (0<x≤10);
(3)如果△DQC是等腰三角形,
①如果DQ=CD=5,
∵∠QDC=∠B,
过C作CG⊥DQ于G,如图2,
∴DG=AH=4,DG=3,
∴QG=2,
∴CQ=$\sqrt{C{G}^{2}+G{Q}^{2}}$=2$\sqrt{5}$;
②如果CQ=CD,
∴CQ=5,
③如果DQ=CQ,
过Q作QL⊥CD于L,如图3,
∴DL=CL=$\frac{5}{2}$,
∵tan∠CDQ=tanB=$\frac{4}{3}$,
∴QL=$\frac{10}{3}$,
∴CQ=$\sqrt{C{L}^{2}+L{Q}^{2}}$=$\frac{25}{6}$,
综上所述:如果△DQC是等腰三角形,CQ的长是2$\sqrt{5}$或5或$\frac{25}{6}$.
点评 本题主要考查了等腰梯形的性质,相似三角形的判定与性质,勾股定理,以及解直角三角形,综合性较强,需要结合图形,对各知识点综合考虑并灵活运用方能解决.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,那么他一次就能猜中的概率是$\frac{1}{5}$.
在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,那么他一次就能猜中的概率是$\frac{1}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
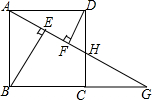 如图,四边形ABCD是正方形,G是BC的延长线上一点,连接AG交CD于点H,BE⊥AG于点E,DF⊥AG于点F.
如图,四边形ABCD是正方形,G是BC的延长线上一点,连接AG交CD于点H,BE⊥AG于点E,DF⊥AG于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com