

���� ��1�����B��C����������������߽���ʽ���ⷽ���鼴�ɣ�
��2�����ۣ��߶�PQ�ij��ȱ��ֲ��䣮�軬����ĵ�P����Ϊ��2-h��k������ƽ�ƺ��QΪ��4-h��-2+k���������������빫ʽ���㼴�ɽ�����⣮
��3��������ͼ2�У�����P���߶�CE���ӳ�����ʱ����Q���߶�CE��ʱ����QE=t���ɡ�PED�ס�ACQ����$\frac{ED}{CQ}$=$\frac{EP}{AC}$���ⷽ�̼��ɽ�����⣮
�ڵ���Q��EC���ӳ�����ʱ����PED�ס�ACQ����PC=t���������ƣ�
��� �⣺��1����D��-2��2����
��DE=OE=2��
��RT��ABC�Ƶ�B��ʱ����ת�õ�RT��DBE��
��RT��ABC��RT��DBE����EBC=90�㣬
��AC=DE��BC=BE���ı���OBCAΪ���Σ�
��AC=DE=OB=2��BC=BE=4��
��B��0��-2����C��4��-2����E��0��2����
��B��0��-2����C��4��-2������y=-$\frac{1}{2}$x2+bx+c��
��$\left\{\begin{array}{l}{c=-2}\\{-8+4b+c=-2}\end{array}\right.$�����$\left\{\begin{array}{l}{b=2}\\{c=-2}\end{array}\right.$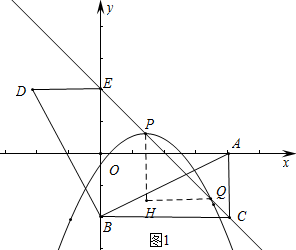
�������߽���ʽΪy=-$\frac{1}{2}$x2+2x-2��
��2�����ۣ��߶�PQ�ij��ȱ��ֲ��䣮
��y=-$\frac{1}{2}$x2+2x-2=-$\frac{1}{2}$��x-2��2��
�軬����ĵ�P����Ϊ��2-h��k������ƽ�ƺ��QΪ��4-h��-2+k����
�ֱ����P��Q��x�ᡢy��Ĵ��߽��ڵ�H��
�ɹ��ɶ�����֪��PQ=$\sqrt{[2-h-��4-h��]^{2}+[k-��-2+k��]^{2}}$=$\sqrt{4+4}$=2$\sqrt{2}$��
��3������ͼ2�У�����P���߶�CE���ӳ�����ʱ����Q���߶�CE��ʱ����QE=t��
��EP=2$\sqrt{2}$-t��CQ=4$\sqrt{2}$-t��
��EP��CQ����PED=��ACQ=45�㣬���PED�ס�ACQ��
��$\frac{ED}{CQ}$=$\frac{EP}{AC}$��
��$\frac{2}{4\sqrt{2}-t}$=$\frac{2\sqrt{2}-t}{2}$��
��t2-6$\sqrt{2}$t+12=0��
���t=3$\sqrt{2}$��$\sqrt{6}$��
��3$\sqrt{2}$+$\sqrt{6}$��2$\sqrt{2}$������������������
��t=3$\sqrt{2}$-$\sqrt{6}$��
��ʱEP=$\sqrt{6}$-$\sqrt{2}$��
��$\frac{\sqrt{2}}{2}$EP=$\sqrt{3}$-1��
���P������1-$\sqrt{3}$��$\sqrt{3}$+1����
�ڵ���Q��EC���ӳ�����ʱ����PED�ס�ACQ����PC=t��
��EP=4$\sqrt{2}$-t��CQ=2$\sqrt{2}$-t��
��$\frac{ED}{CQ}$=$\frac{EP}{AC}$��
��$\frac{2}{2\sqrt{2}-t}$=$\frac{4\sqrt{2}-t}{2}$��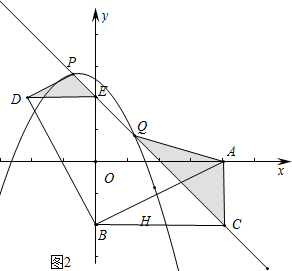
���t=3$\sqrt{2}$-$\sqrt{6}$��3$\sqrt{2}$+$\sqrt{6}$����������
��ʱEP=$\sqrt{6}$+$\sqrt{2}$��
$\frac{\sqrt{2}}{2}$EP=$\sqrt{3}$+1��
��P2��$\sqrt{3}$+1��1-$\sqrt{3}$����
�����������������ĵ�P����ΪP1��1-$\sqrt{3}$��$\sqrt{3}$+1����P2��$\sqrt{3}$+1��1-$\sqrt{3}$����
���� ���⿼��һ�κ����ۺ��⡢��ת�任�����������ε��ж������ʵ�֪ʶ������Ĺؼ������Ӧ�ô���ϵ����ȷ����������ʽ��ѧ�����ò���������⣬ѧ��������ۣ������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ڲ�һ��Ʒ�۸����Ϸ�У����������Ȳ�֪������Ʒ�ļ۸�������Ҫ��������ͼ�����ſ�Ƭ�������������ţ�ʹʣ�µĿ�Ƭ����������һ����λ���������������µļ۸������Ʒ�ļ۸���50Ԫ����ô��һ�ξ��ܲ��еĸ�����$\frac{1}{5}$��
�ڲ�һ��Ʒ�۸����Ϸ�У����������Ȳ�֪������Ʒ�ļ۸�������Ҫ��������ͼ�����ſ�Ƭ�������������ţ�ʹʣ�µĿ�Ƭ����������һ����λ���������������µļ۸������Ʒ�ļ۸���50Ԫ����ô��һ�ξ��ܲ��еĸ�����$\frac{1}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
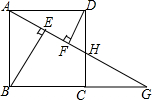 ��ͼ���ı���ABCD�������Σ�G��BC���ӳ�����һ�㣬����AG��CD�ڵ�H��BE��AG�ڵ�E��DF��AG�ڵ�F��
��ͼ���ı���ABCD�������Σ�G��BC���ӳ�����һ�㣬����AG��CD�ڵ�H��BE��AG�ڵ�E��DF��AG�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �����ɸ���ͬ��С�������ɵ�һ����������ͼ��ʾ�����ĸ���ͼΪ��������
�����ɸ���ͬ��С�������ɵ�һ����������ͼ��ʾ�����ĸ���ͼΪ��������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��1 | B�� | x��1 | C�� | x��1 | D�� | x��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{3}$ | B�� | -3 | C�� | 3 | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com