
【题目】二次函数![]() 的图像如图,下列结论:①
的图像如图,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .正确的个数为( )
.正确的个数为( )
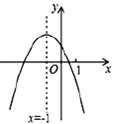
A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
由抛物线的开口方向,抛物线与y轴交点的位置、对称轴即可确定a、b、c的符号,即可对①进行判断;由抛物线与x轴有两个交点判断②即可;由抛物线的对称轴为直线x=-1,可得a=![]() ,当x=1时,y=a+b+c<0,把a=
,当x=1时,y=a+b+c<0,把a=![]() 代入即可对③进行判断;把x=-1代入方程即可求得相应的y的符号,可对④进行判断;综上即可得答案.
代入即可对③进行判断;把x=-1代入方程即可求得相应的y的符号,可对④进行判断;综上即可得答案.
∵抛物线开口向下,与y轴交于正半轴,
∴a<0,c>0,
∵对称轴为直线x=![]() =-1,
=-1,
∴b<0,
∴abc>0,故①正确,
∵抛物线与x轴有两个交点,
∴b2-4ac>0,即4ac-b2<0,故②正确,
∵![]() =-1,
=-1,
∴a=![]() ,
,
∵x=1时,a+b+c<0,
∴![]() +b+c<0,即3b+2c<0,故③正确,
+b+c<0,即3b+2c<0,故③正确,
当x=-1时,a-b+c>0,故④正确,
综上所述:正确的结论有①②③④共4个,
故选D.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】问题探究:
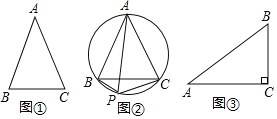
(1)已知:如图①,△ABC中请你用尺规在BC边上找一点D,使得点A到点BC的距离最短.
(2)托勒密(Ptolemy)定理指出,圆的内接四边形两对对边乘积的和等于两条对角线的乘积.如图②,P是正△ABC外接圆的劣弧BC上任一点(不与B、C重合),请你根据托勒密(Ptolemy)定理证明:PA=PB+PC
问题解决:
(3)如图③,某学校有一块两直角边长分别为30m、60m的直角三角形的草坪,现准备在草坪内放置一对石凳及垃圾箱在点P处,使P到A、B、C三点的距离之和最小,那么是否存在符合条件的点P?若存在,请作出点P的位置,并求出这个最短距离(结果保留根号);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件30元,售价为每件40元,每周可卖出180件;如果每件商品的售价每上涨1元,则每周就会少卖出5件,但每件售价不能高于50元,设每件商品的售价上涨x元(x为整数),每周的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每件商品的售价为多少元时,每周可获得最大利润?最大利润是多少?
(3)每件商品的售价定为多少元时,每周的利润恰好是2145元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】历下区历史文化悠久,历下一名,取意于大舜帝耕作于历山之下。这位远古圣人为济南留下了影响深远的大舜文化,至今已绵延两千年.某校就同学们对“舜文化”的了解程度进行随机抽样调查,将调查结果绘制成如下两幅统计图:
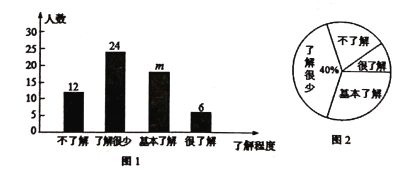
根据统计图的信息,解答下列问题:
(1)本次共调查 名学生,条形统计图中![]() ;
;
(2)若该校共有学生1200名,请估算该校约有多少名学生不了解“舜文化”;
(3)谓查结果中,该校九年级(2)班有四名同学相当优秀,了解程度为“很了解”,他们是三名男生、—名女生,现准备从这四名同学中随机抽取两人去市里参加“舜文化”知识竞赛,用树状或列表法,求恰好抽中一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() 经过
经过![]() 两点,交
两点,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
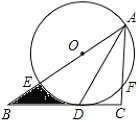
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径是
的半径是![]() ,
,![]() 是弧
是弧![]() 的中点,求阴影部分的面积(结果保留
的中点,求阴影部分的面积(结果保留![]() 和根号).
和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一声汽笛长鸣,火车开进了蔡家崖.这是我省吕梁革命老区人民期盼已久的客运列车.蔡家崖列车的开通.带动老区驶入了发展红色旅游的快车进.某旅行社对去年“国庆”期间到吕梁观光的游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,回答下列问题:

(1)求本次抽样调查的总人数:
(2)补全条形统计图;
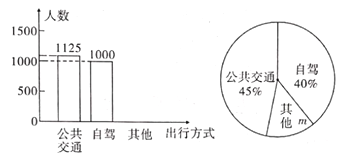
(3)扇形统计图中“其他”部分扇形的圆心角度数为____;
(4)去年“国庆”期问到吕梁观光的旅游者为275万人,则选择自驾方式出行的有多少万人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“书”、“ 香”、“ 历”、“ 城”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.
(1)若从中任取一个球,球上的汉字刚好是 “书”的概率为__________.
(2)从中任取一球,不放回,再从中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字能组成“历城”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com