【题目】将一幅三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．
（1）求证：CF∥AB．
（2）求∠DFC的度数．
【答案】解：（1）证明：∵CF平分∠DCE，∴∠1=∠2=
∠DCE。
∵∠DCE=90°，∴∠1=45°。
∵∠3=45°，∴∠1=∠3。∴AB∥CF。
（2）∵∠D=30°，∠1=45°，
∴∠DFC=180°﹣30°﹣45°=105°。
【解析】
试题（1）首先根据角平分线的性质可得∠1=45°，再有∠3=45°，再根据内错角相等两直线平行可判定出AB∥CF；
（2）利用三角形内角和定理进行计算即可．
试题解析：（1）∵CF平分∠DCE，∴∠1=∠2=∠DCE，∵∠DCE=90°，∴∠1=45°，∵∠3=45°，∴∠1=∠3，∴AB∥CF（内错角相等，两直线平行）；
（2）∵∠D=30°，∠1=45°，∴∠DFC=180°﹣30°﹣45°=105°．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】如图，∠1和∠2互补，∠C=∠EDF．
（1）判断DF与EC的关系为 ．
（2）试判断DE与BC的关系，并说明理由．
（3）试判断∠DEC与∠DFC的关系并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB∥CD，∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H，∠K﹣∠H=27°，则∠K=（ ）
A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目：初中数学 来源： 题型：
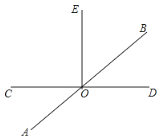
【题目】如图，已知直线AB和CD相交于点O，在∠COB的内部作射线OE.
（1）若∠AOC=36°，∠COE=90°，求∠BOE的度数；
（2）若∠COE：∠EOB：∠BOD=4：3：2，求∠AOE的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，以AC为直径作⊙O交BC于点D，交AB于点G，且D是BC中点，DE⊥AB，垂足为E，交AC的延长线于点F．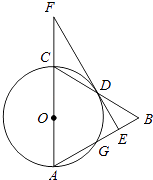 
（1）求证：直线EF是⊙O的切线；
（2）若CF=5，cosA= 
，求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列命题：①对顶角相等；②同位角相等，两直线平行；③若|a|＝|b|，则a＝b；④若x＝2，则2|x|－1＝3.以上命题是真命题的有( ).
A. ①②③④ B. ①④ C. ②④ D. ①②④
查看答案和解析>>
科目：初中数学 来源： 题型：
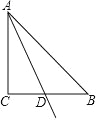
【题目】如图，在等腰 Rt△ABC 中，AC=BC=2，点 D 是 BC 的中点，P 是射线 AD 上的一个动点，则当△BPC 为直角三角形时，AP 的长为____________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD∥BC，∠A=90°，E是AB上的一点，且AD=BE，∠1=∠2．
（1）求证：△ADE≌△BEC；
（2）若AD=6，AB=14，请求出CD的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com