
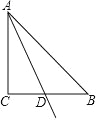
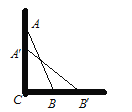
【题目】如图,在等腰 Rt△ABC 中,AC=BC=2,点 D 是 BC 的中点,P 是射线 AD 上的一个动点,则当△BPC 为直角三角形时,AP 的长为____________.
【答案】0或![]() -1或
-1或![]() +1或2
+1或2![]()
【解析】
①当P点与A点重合时,AP=0;②在Rt△ADC中利用勾股定理即可求出AD的长度,再根据直角三角形中斜边上的中线等于斜边的一半即可求出DP的长度,由线段间的关系即可得出AP的长度;当∠CBP=90°时,△PBD≌△ACD,则AD=PD,进一步得到AP的长度.
①当P点与A点重合时,AP=0,
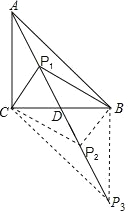
②依照题意画出图形,如图所示.
∵∠ACB=90°,AC=BC=2,D是BC的中点,
∴CD=BD=![]() BC=1,AD=
BC=1,AD=![]() =
=![]() .
.
∵∠BPC=90°,D是BC的中点,
∴DP=![]() BC=1,
BC=1,
∴AP1=ADDP1=![]() 1或AP2=AD+DP2=
1或AP2=AD+DP2=![]() +1.
+1.
当∠CBP3=90°时,△P3BD≌△ACD,
则AD=P3D,
则AP3=2AD=2![]() .
.
故答案为:0或![]() +1或
+1或![]() 1或2
1或2![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)的图象过点P(﹣ ![]() ,0),且与反比例函数y=
,0),且与反比例函数y= ![]() (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B. 
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
查看答案和解析>>
科目:初中数学 来源: 题型:
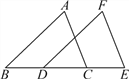
【题目】如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).
查看答案和解析>>
科目:初中数学 来源: 题型:
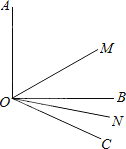
【题目】如图所示,已知∠AOB=90°,∠BOC=20°,OM平分∠AOC,ON平分∠BOC;
(1)求∠MON;
(2)∠AOB=α,∠BOC=β,求∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一架长2.5米的梯子AB如图所示斜靠在一面墙上,这时梯足B离墙底C(∠C=90°)的距离BC为0.7米.
(1)求此时梯顶A距地面的高度AC;
(2)如果梯顶A下滑0.9米,那么梯足B在水平方向,向右滑动了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民用水实行阶梯水价,实施细则如下表:
分档水量 | 年用水量 (立方米) | 水价 (元/立方米) |
第一阶梯 | 0~180(含) | 5.00 |
第二阶梯 | 181~260(含) | 7.00 |
第三阶梯 | 260以上 | 9.00 |
例如,某户家庭年使用自来水200 m3,应缴纳:180×5+(200-180)×7=1040元;
某户家庭年使用自来水300 m3,应缴纳:180×5+(260-180)×7+(300-260)×9=1820元.
(1)小刚家2017年共使用自来水170 m3,应缴纳 元;小刚家2018年共使用自来水260 m3,应缴纳 元.
(2)小强家2018年使用自来水共缴纳1180元,他家2018年共使用了多少自来水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P. 
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60,得到△BAE,连接ED,若BC=5,BD=4,则有以下四个结论:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC。其中正确结论的序号是( )
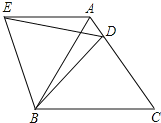
A. ②③④ B. ①③④ C. ①②④ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com