
【题目】如图,菱形![]() 的周长为
的周长为![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() ,则下列结论中正确的个数为( )
,则下列结论中正确的个数为( )
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.

A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】
连接AC交BD于O,由菱形的性质求出边长,设AE=4x,DE=3x,根据勾股定理得出方程,解方程求出x,得出AE、DE,由菱形的面积=底×高,求出菱形的面积;根据勾股定理求出BD,得出OD,再由勾股定理求出OA,得出AC,即可得出结论.
连接AC交BD于O,如图所示:
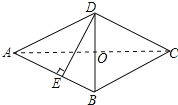
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,AC⊥BD,
BD,AC⊥BD,
∵菱形ABCD的周长为20cm,
∴AD=AB=5cm,
∵DE⊥AB,AE:DE=4:3,
则∠AED=90°,
设AE=4xcm,DE=3xcm,
根据勾股定理得:(4x)2+(3x)2=52,
解得:x=1,
∴AE=4cm,DE=3cm,
∴BE=5-4=1,S菱形=ABDE=5×3=15(cm2),
∴①②③正确;
在Rt△BDE中,根据勾股定理得:BD=![]() ,
,
∴OD=![]() ,
,
在Rt△AOD中,OA=![]() ,
,
∴AC=2OA=3![]() ,
,
∴④不正确;
故选B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 如图摆放,边
如图摆放,边![]() 与
与![]() 重合,
重合,![]() .当点
.当点![]() 从点
从点![]() 出发沿
出发沿![]() 方向滑动时,点
方向滑动时,点![]() 同时从点
同时从点![]() 出发沿
出发沿![]() 轴正方向滑动.
轴正方向滑动.
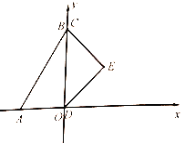
![]() 设点
设点![]() 关于
关于![]() 的函数表达式为________.
的函数表达式为________.
![]() 连接
连接![]() .当点
.当点![]() 从点
从点![]() 滑动到点
滑动到点![]() 时,
时,![]() 的面积最大值为_______.
的面积最大值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1═![]() (x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
(3)设m=![]() ,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)的长方形ABCD中,E点在AD上,且BE=2AE.今分别以BE、CE为折线,将A、D向BC的方向折过去,图(2)为对折后A、B、C、D、E五点均在同一平面上的位置图.若图(2)中,∠AED=15°,则∠BCE的度数为_____.
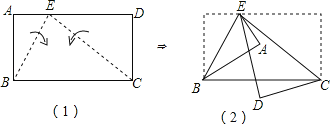
查看答案和解析>>
科目:初中数学 来源: 题型:
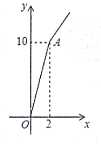
【题目】某玉米种子的价格为![]() 元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为
元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为![]() ,请你结合表格和图象:
,请你结合表格和图象:
付款金额 |
| 7.5 | 10 | 12 |
|
购买量 | 1 | 1.5 | 2 | 2.5 | 3 |
(1)![]() ,
,![]() ;
;
(2)求出当![]() 时,
时,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图1,点D在线段BC的延长线上移动,若∠BAC=30°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β:
①如图1,当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
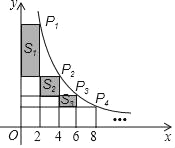
【题目】如图,在反比例函数y=![]() (x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为2,4,6,8,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn=_____(用含n的代数式表示)
(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为2,4,6,8,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn=_____(用含n的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com