

分析 (1)由图形即可得出结论;
(2)通过不断的寻找全等三角形来寻找∠BAF=∠CAF这个条件,通过三次全等三角形的证明可得出此结论;
(3)同(2)的道理,通过三次全等三角形的证明,得出∠EAO=∠BAO,从而由边角关系求出∠AFC的度数.
解答 解:(1)根据已知条件可证得△ABF≌△ACF,可得知∠AFB=∠AFC,
∴∠AFC=90°.
故答案为:90°
(2)证明:连接BD,CE,如图1.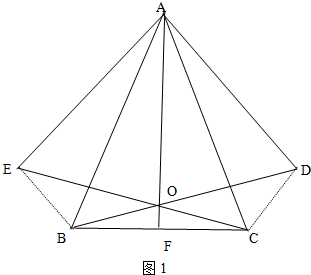
∵等腰△ABC中,AB=AC,△ABD、△ACE都是等边三角形,
∴AE=AC=AD=AB,∠EAC=∠DAB=60°,
∴∠EAB=∠DAC,
在△EAB和△DAC中,$\left\{\begin{array}{l}{AE=AD}\\{∠EAB=∠DAC}\\{AB=AC}\end{array}\right.$,
∴△EAB≌△DAC(SAS),
∴∠ABE=∠ACD,BE=CD,
∵△ABC为等腰三角形,
∴∠ABC=∠ACB,
∴∠EBC=∠ABE+∠ABC=∠ACD+∠ACB=∠DCB,
在△BCE和△CBD中,$\left\{\begin{array}{l}{BE=CD}\\{∠EBC=∠DCB}\\{BC=CB}\end{array}\right.$,
∴△EBC≌△DCB(SAS),
∴∠ECB=∠DBC,
∴OB=OC,
在△ABO和△ACO,$\left\{\begin{array}{l}{AB=AC}\\{AO=AO}\\{BO=CO}\end{array}\right.$,
∴△ABO≌△ACO(SSS),
∴∠BAF=∠CAF,
∴AF⊥BC.
证毕.
(3)令AE与BD的交点为M,AB与CE的交点为N,如图2,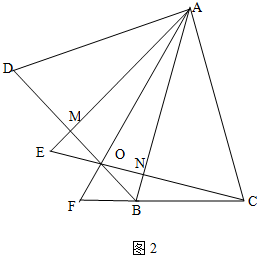
∵∠CAN=60°-∠MAN=∠DAM,
∴在△ADM和△ACN中,$\left\{\begin{array}{l}{∠CAN=∠DAM}\\{AD=AB=AC}\\{∠ADM=∠ACN=60°}\end{array}\right.$,
∴△ADM≌△ACN(ASA),
∴AM=AN,
又∵AE=AC=AB,
∴ME=NB,
在△EOM和△BON中,$\left\{\begin{array}{l}{∠MEO=∠NBO=60°}\\{∠MOE=∠NOB}\\{ME=NB}\end{array}\right.$,
∴△EOM≌△BON(AAS),
∴OM=ON,
在△AMO和△ANO中,$\left\{\begin{array}{l}{AM=AN}\\{AO=AO}\\{OM=ON}\end{array}\right.$,
∴△AMO≌△ANO,
∴∠MAO=∠NAO,
∴∠BAC=60°-∠MAN=60°-2∠NAO,
∵AB=AC,
∴∠ACB=(180°-∠BAC)÷2=(180°-60°+2∠NAO)÷2=60°+∠NAO,
又∵∠ABC=∠AFB+∠NAO=∠ACB,
∴∠AFB=60°
点评 本题考查的全等三角形的证明,(2)解题的关键是通过证三角形全等得出∠BAF=∠CAF,从而得出结论;(3)解题的关键是通过证三角形全等得出∠MAO=∠NAO,再利用三角形内角和为180°和三角形外角等于不相邻的两内角和得出结论.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:填空题
 如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数),那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是$\sqrt{2}$.
如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数),那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,D为BC上一点,E为AD延长线上一点,BD:DC=5:3,∠C=∠E,若AD=4,BC=8,则DE的长为( )
如图,在△ABC中,D为BC上一点,E为AD延长线上一点,BD:DC=5:3,∠C=∠E,若AD=4,BC=8,则DE的长为( )| A. | $\frac{15}{4}$ | B. | $\frac{15}{3}$ | C. | 5 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,A、B、C是同一直线上的依次三点,下列说法正确的是( )
如图所示,A、B、C是同一直线上的依次三点,下列说法正确的是( )| A. | 射线AB与射线BA是同一条射线 | B. | 射线BA与射线BC是同一条射线 | ||
| C. | 射线AB与射线AC是同一条射线 | D. | 直线BA与直线BC不是同一条直线 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
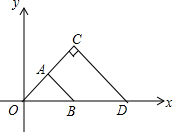 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为(1,1).
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为(1,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com