
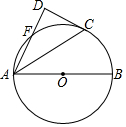
 如图.⊙O的半径为5,AB为⊙O直径,C,F为⊙O上的两点,AF,AC为⊙O的弦.
如图.⊙O的半径为5,AB为⊙O直径,C,F为⊙O上的两点,AF,AC为⊙O的弦.分析 (1)若点F、C将圆三等分,则∠AOC=120°,过点O作OE⊥AC于点E,利用含30度的直角三角形的性质即可求出AC的长度.
(2)连接BF、CB,OC,由于CD是⊙O的切线,所以OC∥AD,
解答 解:(1)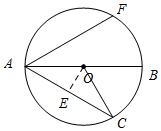 当F、C把圆三等分后,
当F、C把圆三等分后,
此时∠AOC=120°,
过点O作OE⊥AC于点E,
∵OA=OC,
∴∠OAC=30°,
∴OE=$\frac{1}{2}$OA=$\frac{5}{2}$,
由勾股定理可知:AE=$\frac{5}{2}\sqrt{3}$,
由垂径定理可知:AC=2AE=5$\sqrt{3}$,
(2)连接BF、CB,
连接OC角BF于点E,
∵CD是⊙O的切线,
∴∠DCO=90°,
∵点C平分$\widehat{FB}$,
∴∠DAC=∠BAC,
∵OA=OC,
∴∠BAC=∠ACO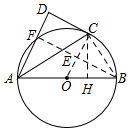
∴∠DAC=∠ACO,
∴OC∥AD,
∴∠D=90°,
过点C作CH⊥AB于点H,
∴DC=HC=4,
由勾股定理可知:OH=3,
∴AH=OH+OA=8,
∴由勾股定理可知:AC2=80
∴△ADC∽△ACB
∴$\frac{CD}{CB}=\frac{AC}{AB}$=$\frac{AD}{AC}$,
∴AC2=AB•AD
∴AD=8
∵点C平分$\widehat{FB}$,
∴由垂径定理可知OC⊥BF
∴∠CEB=∠CHB=90°
∴∠OCH=∠OBE
在△COH与△EBO中
$\left\{\begin{array}{l}{∠OHC=∠BEO}\\{∠OCH=∠OBE}\\{OC=OB}\end{array}\right.$,
∴△COH≌△EBO(AAS)
∴CH=EB=4,OH=OE=3,
∴AF=2OE=6,
∴DF=AD-AF=2
点评 本题考查圆的综合问题,涉及全等三角形的性质与判定,相似三角形的性质与判定,垂径定理,勾股定理等知识,题目较为综合,本题属于中等题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
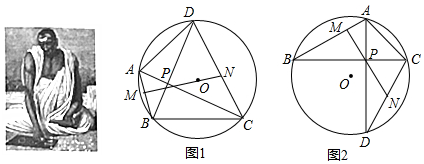
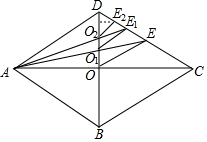 如图所示,菱形ABCD的对角线AC,BD交于点O,AB=8,∠DAB=60°,过点O作OE∥BC交CD于点E,连接AE交BD于点O1,过点O1作O1E1∥BC交CD于点E1…依此规律进行下去,则S${\;}_{△A{O}_{n}{E}_{n}}$=S${\;}_{△D{O}_{n}{E}_{n}}$(填入″>″、″=″或″<″),△AOnEn的面积是($\frac{4}{9}$)n•4$\sqrt{3}$.
如图所示,菱形ABCD的对角线AC,BD交于点O,AB=8,∠DAB=60°,过点O作OE∥BC交CD于点E,连接AE交BD于点O1,过点O1作O1E1∥BC交CD于点E1…依此规律进行下去,则S${\;}_{△A{O}_{n}{E}_{n}}$=S${\;}_{△D{O}_{n}{E}_{n}}$(填入″>″、″=″或″<″),△AOnEn的面积是($\frac{4}{9}$)n•4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一枚硬币,正面朝上 | |
| B. | 任意三条线段可以组成一个三角形 | |
| C. | 投掷一枚质地均匀的骰子,掷得的点数是奇数 | |
| D. | 13人中至少有两个人出生的月份相同 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com