
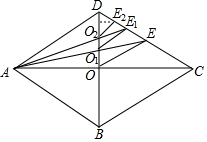
 如图所示,菱形ABCD的对角线AC,BD交于点O,AB=8,∠DAB=60°,过点O作OE∥BC交CD于点E,连接AE交BD于点O1,过点O1作O1E1∥BC交CD于点E1…依此规律进行下去,则S${\;}_{△A{O}_{n}{E}_{n}}$=S${\;}_{△D{O}_{n}{E}_{n}}$(填入″>″、″=″或″<″),△AOnEn的面积是($\frac{4}{9}$)n•4$\sqrt{3}$.
如图所示,菱形ABCD的对角线AC,BD交于点O,AB=8,∠DAB=60°,过点O作OE∥BC交CD于点E,连接AE交BD于点O1,过点O1作O1E1∥BC交CD于点E1…依此规律进行下去,则S${\;}_{△A{O}_{n}{E}_{n}}$=S${\;}_{△D{O}_{n}{E}_{n}}$(填入″>″、″=″或″<″),△AOnEn的面积是($\frac{4}{9}$)n•4$\sqrt{3}$. 分析 利用平行线的性质,平行线间的距离相等,可得S${\;}_{△A{O}_{n}{E}_{n}}$=S${\;}_{△D{O}_{n}{E}_{n}}$,由△DO1E1∽△DOE,推出$\frac{{S}_{△D{O}_{1}{E}_{1}}}{{S}_{△DOE}}$=($\frac{2}{3}$)2=$\frac{4}{9}$,探究规律后,利用规律即可解决问题.
解答 解:①∵OnEn∥AD,
∴S${\;}_{△A{O}_{n}{E}_{n}}$=S${\;}_{△D{O}_{n}{E}_{n}}$,
故答案为=.
②∵四边形ABCD是菱形,
∴AB=BC=CD=AD=8,
∵∠DAB=60°,
∴△ADB和△BDC都是等边三角形,
∴∠DCO=30°,
在Rt△DOC中,∵∠DOC=90°,∠DCO=30°,
∴OD=$\frac{1}{2}$CD=4,OC=$\sqrt{C{D}^{2}-O{D}^{2}}$=4$\sqrt{3}$,
∴S△DOC=$\frac{1}{2}$•OD•OC=$\frac{1}{2}$$•4•4\sqrt{3}$=8$\sqrt{3}$,
∵OE∥AD,OA=OC,
∴DE=EC,
∴S△DOE=$\frac{1}{2}$S△DOC=4$\sqrt{3}$,
∵OE∥AD,
∴$\frac{O{O}_{1}}{D{O}_{1}}$=$\frac{OE}{D{O}_{1}}$=$\frac{1}{2}$,
∵O1E1∥OE,
∴△DO1E1∽△DOE,
∴$\frac{{S}_{△D{O}_{1}{E}_{1}}}{{S}_{△DOE}}$=($\frac{2}{3}$)2=$\frac{4}{9}$,
∴${S}_{△D{O}_{1}{E}_{1}}$=$\frac{4}{9}$•4$\sqrt{3}$,
同理,${S}_{△D{O}_{2}{E}_{2}}$=$\frac{4}{9}$•${S}_{△D{O}_{1}{E}_{1}}$=($\frac{4}{9}$)2•4$\sqrt{3}$,
…,
∴${S}_{△D{O}_{n}{E}_{n}}$=($\frac{4}{9}$)n•4$\sqrt{3}$,
∴S${\;}_{△A{O}_{n}{E}_{n}}$=S${\;}_{△D{O}_{n}{E}_{n}}$=($\frac{4}{9}$)n•4$\sqrt{3}$.
故答案为($\frac{4}{9}$)n•4$\sqrt{3}$.
点评 本题考查菱形的性质、平行线的性质、等边三角形的判定和性质、三角形的面积公式等知识,解题的关键是学会从特殊到一般的探究规律,学会利用规律解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF,下面四个结论:①$\frac{FG}{FB}$=$\frac{1}{2}$;②点F是GE的中点;③AF=$\frac{\sqrt{2}}{3}$AB;④S△ABC=6S△BDF.其中正确结论的序号是①③④.
如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF,下面四个结论:①$\frac{FG}{FB}$=$\frac{1}{2}$;②点F是GE的中点;③AF=$\frac{\sqrt{2}}{3}$AB;④S△ABC=6S△BDF.其中正确结论的序号是①③④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
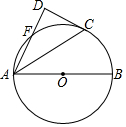 如图.⊙O的半径为5,AB为⊙O直径,C,F为⊙O上的两点,AF,AC为⊙O的弦.
如图.⊙O的半径为5,AB为⊙O直径,C,F为⊙O上的两点,AF,AC为⊙O的弦.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-4)2=21 | B. | (x-4)2=11 | C. | (x+4)2=21 | D. | (x+4)2=11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com