
 如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF,下面四个结论:①$\frac{FG}{FB}$=$\frac{1}{2}$;②点F是GE的中点;③AF=$\frac{\sqrt{2}}{3}$AB;④S△ABC=6S△BDF.其中正确结论的序号是①③④.
如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF,下面四个结论:①$\frac{FG}{FB}$=$\frac{1}{2}$;②点F是GE的中点;③AF=$\frac{\sqrt{2}}{3}$AB;④S△ABC=6S△BDF.其中正确结论的序号是①③④. 分析 首先根据题意易证得△ABG≌△BCD(ASA),则AG=BD,AG=$\frac{1}{2}$AB,根据相似三角形的对应边成比例与BA=BC,继而证得$\frac{AG}{AB}$=$\frac{FG}{FB}$=$\frac{1}{2}$;正确;继而可得FG=$\frac{1}{2}$BF;即可得AF=$\frac{1}{3}$AC,又由等腰直角三角形的性质,可得AC=$\frac{\sqrt{2}}{3}$AB,即可求得AF=$\frac{\sqrt{2}}{3}$AB;则可得S△ABC=6S△BDF.
解答 解:∵∠ABC=90°,BG⊥CD,
∴∠DBE+∠BDE=∠BDE+∠BCD=90°,
∴∠DBE=∠BCD,
在△ABG和△BCD中$\left\{\begin{array}{l}{∠GAB=∠CBD}\\{AB=BC}\\{∠ABG=∠BCD}\end{array}\right.$,
∴△ABG≌△BCD(ASA),
则AG=BD,
∵在Rt△ABC中,∠ABC=90°,
∴AB⊥BC,AG⊥AB,
∴AG∥BC,
∴△AFG∽△CFB,
∴$\frac{AG}{CB}$=$\frac{FG}{FB}$=$\frac{1}{2}$,
故①正确;
∵AB=CB,点D是AB的中点,
∴BD=$\frac{1}{2}$AB=$\frac{1}{2}$CB,
∵tan∠BCD=$\frac{BD}{BC}$=$\frac{1}{2}$,
∴在Rt△ABG中,tan∠DBE=$\frac{AG}{AB}$=$\frac{1}{2}$,
∵$\frac{AG}{AB}$=$\frac{1}{2}$,
∴FG=$\frac{1}{2}$FB,
∵GE≠BF,
∴点F不是GE的中点.
故②错误;
∵△AFG∽△CFB,
∴AF:CF=AG:BC=1:2,
∴AF=$\frac{1}{3}$AC,
∵AC=$\sqrt{2}$AB,
∴AF=$\frac{\sqrt{2}}{3}$AB,
故③正确;
∵BD=$\frac{1}{2}$AB,AF=$\frac{1}{3}$AC,
∴S△ABC=6S△BDF,
故④正确.
故答案为:①③④.
点评 此题考查了相似三角形的判定与性质、直角三角形的性质以及三角函数等知识.此题难度适中,解题的关键是证得△AFG∽△CFB,注意掌握数形结合思想与转化思想的应用.


科目:初中数学 来源: 题型:解答题
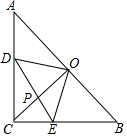 在Rr△ABC中,∠C=90°,AC=BC=1,点O为AB的中点,点D、E分别为AC、AB边上的动点,且保持DO⊥EO,连接CO、DE交于点P.
在Rr△ABC中,∠C=90°,AC=BC=1,点O为AB的中点,点D、E分别为AC、AB边上的动点,且保持DO⊥EO,连接CO、DE交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
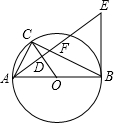 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,经过点A作AE⊥OC,垂足为点D,AE与BC交于点F,与过点B的直线交于点E,且EB=EF.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,经过点A作AE⊥OC,垂足为点D,AE与BC交于点F,与过点B的直线交于点E,且EB=EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
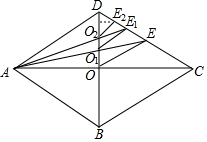 如图所示,菱形ABCD的对角线AC,BD交于点O,AB=8,∠DAB=60°,过点O作OE∥BC交CD于点E,连接AE交BD于点O1,过点O1作O1E1∥BC交CD于点E1…依此规律进行下去,则S${\;}_{△A{O}_{n}{E}_{n}}$=S${\;}_{△D{O}_{n}{E}_{n}}$(填入″>″、″=″或″<″),△AOnEn的面积是($\frac{4}{9}$)n•4$\sqrt{3}$.
如图所示,菱形ABCD的对角线AC,BD交于点O,AB=8,∠DAB=60°,过点O作OE∥BC交CD于点E,连接AE交BD于点O1,过点O1作O1E1∥BC交CD于点E1…依此规律进行下去,则S${\;}_{△A{O}_{n}{E}_{n}}$=S${\;}_{△D{O}_{n}{E}_{n}}$(填入″>″、″=″或″<″),△AOnEn的面积是($\frac{4}{9}$)n•4$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com