
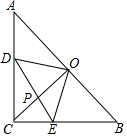
 在Rr△ABC中,∠C=90°,AC=BC=1,点O为AB的中点,点D、E分别为AC、AB边上的动点,且保持DO⊥EO,连接CO、DE交于点P.
在Rr△ABC中,∠C=90°,AC=BC=1,点O为AB的中点,点D、E分别为AC、AB边上的动点,且保持DO⊥EO,连接CO、DE交于点P.分析 (1)证明△ADO≌△CEO,可得OD=OE;
(2)先根据对角互补证明D、C、E、O四点共圆,再得△DPO∽△CPE,列比例式可得:PD•EP=CP•PO,设CP=x,则OP=$\frac{\sqrt{2}}{2}$-x,则CP•PO=x($\frac{\sqrt{2}}{2}-x$)=-${x}^{2}+\frac{\sqrt{2}}{2}x$,根据二次函数的最值问题得出DP•EP存在最大值为$\frac{1}{8}$;
(3)设CE=a,则CD=2a,根据AC=1列等式求出,a=$\frac{1}{3}$,则CE=$\frac{1}{3}$,CD=$\frac{2}{3}$,根据勾股定理求DE的长,作辅助线构建平行线,得相似,列比例式可求得DP的长.
解答 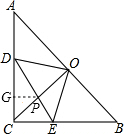 证明:(1)∵AC=BC=1,点O为AB的中点,
证明:(1)∵AC=BC=1,点O为AB的中点,
∴CO⊥AB,CO=AO,
∴∠COA=90°,
∴∠DOP+∠AOD=90°,
∵DO⊥OE,
∴∠DOP+∠POE=90°,
∴∠AOD=∠POE,
同理∠A=∠OCE,
∴△ADO≌△CEO,
∴OD=OE;
(2)∵∠ACB=90°,∠DOE=90°,
∴∠ACB+∠DOE=180°,
∴D、C、E、O四点共圆,
∴∠ODP=∠PCE,∠DPO=∠CPE,
∴△DPO∽△CPE,
∴$\frac{PD}{CP}=\frac{PO}{PE}$,
∴PD•EP=CP•PO,
在Rt△ACB中,AB=$\sqrt{2}$,
∴CO=AO=BO=$\frac{\sqrt{2}}{2}$,
设CP=x,则OP=$\frac{\sqrt{2}}{2}$-x,
则CP•PO=x($\frac{\sqrt{2}}{2}-x$)=-${x}^{2}+\frac{\sqrt{2}}{2}x$=-(x-$\frac{\sqrt{2}}{4}$)2+$\frac{1}{8}$,
即当x=$\frac{\sqrt{2}}{4}$时,CP•PO有最大值为$\frac{1}{8}$,
也就是DP•EP存在最大值为$\frac{1}{8}$;
(3)设CE=a,则CD=2a,
由(1)得:AD=CE=a,
∵AC=1,
∴a+2a=1,
a=$\frac{1}{3}$,
∴CE=$\frac{1}{3}$,CD=$\frac{2}{3}$,
由勾股定理得:DE=$\sqrt{(\frac{1}{3})^{2}+(\frac{2}{3})^{2}}$=$\frac{\sqrt{5}}{3}$,
过P作PG∥BC,交AC于G,
∵∠DCO=45°,
∴PG=CG,
∵PG∥CE,
∴△DGP∽△DCE,
∴$\frac{PG}{CE}=\frac{DG}{DC}$=$\frac{PD}{DE}$,
∴$\frac{PG}{\frac{1}{3}}$=$\frac{\frac{2}{3}-PG}{\frac{2}{3}}$=$\frac{PD}{\frac{\sqrt{5}}{3}}$,
∴PG=$\frac{2}{9}$,PD=$\frac{2\sqrt{5}}{9}$.
点评 本题是三角形的综合题,考查了三角形全等、相似的性质和判定、四点共圆的性质和判定、勾股定理等知识,与二次函数相结合,利用二次函数的最值求线段乘积的最大值,熟练掌握三角形全等和相似的判定方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 过P可画直线垂直于l | B. | 过Q可画直线l的垂线 | ||
| C. | 连结PQ使PQ⊥l | D. | 过Q可画直线与l垂直 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 60 | B. | 30 | C. | 240 | D. | 120 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF,下面四个结论:①$\frac{FG}{FB}$=$\frac{1}{2}$;②点F是GE的中点;③AF=$\frac{\sqrt{2}}{3}$AB;④S△ABC=6S△BDF.其中正确结论的序号是①③④.
如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连接CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF,下面四个结论:①$\frac{FG}{FB}$=$\frac{1}{2}$;②点F是GE的中点;③AF=$\frac{\sqrt{2}}{3}$AB;④S△ABC=6S△BDF.其中正确结论的序号是①③④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com