
分析 (1)首先通分,然后进行减法计算即可;
(2)由$\frac{1}{x}+\frac{1}{y}=\sqrt{5}$(x≠y),变形成x+y=$\sqrt{5}$xy的形式,然后代入化简后的式子计算即可.
解答 解:(1)A=$\frac{{x}^{2}}{xy(x-y)}$-$\frac{{y}^{2}}{xy(x-y)}$
=$\frac{(x+y)(x-y)}{xy(x-y)}$
=$\frac{x+y}{xy}$;
(2)∵$\frac{1}{x}+\frac{1}{y}=\sqrt{5}$,
∴$\frac{x+y}{xy}$=$\sqrt{5}$,即x+y=$\sqrt{5}$xy,
∴A=$\frac{\sqrt{5}xy}{xy}$=$\sqrt{5}$.
点评 本题考查了分式的化简求值,正确对所求的式子进行通分、约分是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
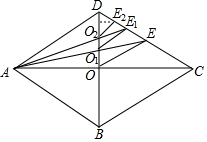 如图所示,菱形ABCD的对角线AC,BD交于点O,AB=8,∠DAB=60°,过点O作OE∥BC交CD于点E,连接AE交BD于点O1,过点O1作O1E1∥BC交CD于点E1…依此规律进行下去,则S${\;}_{△A{O}_{n}{E}_{n}}$=S${\;}_{△D{O}_{n}{E}_{n}}$(填入″>″、″=″或″<″),△AOnEn的面积是($\frac{4}{9}$)n•4$\sqrt{3}$.
如图所示,菱形ABCD的对角线AC,BD交于点O,AB=8,∠DAB=60°,过点O作OE∥BC交CD于点E,连接AE交BD于点O1,过点O1作O1E1∥BC交CD于点E1…依此规律进行下去,则S${\;}_{△A{O}_{n}{E}_{n}}$=S${\;}_{△D{O}_{n}{E}_{n}}$(填入″>″、″=″或″<″),△AOnEn的面积是($\frac{4}{9}$)n•4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
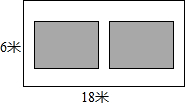 如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为多少米?
如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直的四边形是菱形 | |
| B. | 矩形的对角线相等 | |
| C. | 有两边及一角对应相等的两个三角形全等 | |
| D. | 平行四边形是轴对称图形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com