
����Ŀ���ƶ��Ƚ���The International Medals for Outstanding Discoveries in Mathematics���ǹ�����ѧ���˵Ĺ�����ѧ�Ҵ���ϰ䷢�Ľ��ÿ����һ�ΰ����Խ����������ѧ�ң��ý������ڸ���Ԫ��ǰδ����ʮ�ꡣ�ƶ��Ƚ�����Ϊ��ѧ���ŵ�������������и���������ͼ�ǽ�ֹ��2002��44λ�Ѷ��Ƚ�������ʱ������ͳ��ͼ��������ƶ��Ƚ�������ʱ��ƽ��������35�ꡣ���������ͼ�ش����⣺
��1���Ѷ��Ƚ�������ʱ������������λ�����ж����ˣ�
��2���Ѷ��Ƚ�������ʱ����������Ƕ��٣�
��3���Ѷ��Ƚ�������ʱ����������ƽ�����������ռ�������İٷֱ��Ƕ��٣�
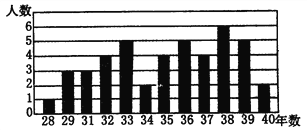
���𰸡���1����λ��Ϊ35.5�꣬���䳬����λ������22�ˣ���2��������38�ꣻ��3��50%��
�������������������1��������ͳ��ͼ�����������ݰ���С�����˳�����У�������λ���Ķ��������������ݵ���λ����������÷Ѷ��Ƚ�������ʱ�����䳬����λ������������2������������һ�������г��ִ����������ݣ����ɵ��������ݵ�������ע���������Բ�ֹһ������3������ƽ������35������Ϊ22�ˣ�������÷Ѷ��Ƚ�������ʱ���������ƽ�����������ռ�������İٷֱȣ�
���������
(1)����λ��Ϊ35.5�꣬
�����䳬����λ������22�ˣ�
(2) ������38�ꣻ
(3)����ƽ�����������Ϊ22����
22��44=50%
���Ѷ��Ƚ�������ʱ���������ƽ�����������ռ�������İٷֱ���50%.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ACB=90����AC=6cm��BC=8cm������M�ӵ�B��������BA������ÿ��3cm���ٶ���A�˶���ͬʱ����N�ӵ�C��������CB������ÿ��2cm���ٶ����B�˶����˶�ʱ��Ϊt�루0��t��![]() ��������MN��
��������MN��
��1������BMN����ABC���ƣ���t��ֵ��
��2������AN��CM����AN��CM����t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC����ADE���ǵ���ֱ���������� ��BAC=��DAE=90��.
��1����ͼ1����D��E��AB��AC������BD��CE����������������ϵ��λ�ù�ϵ?(ֱ��д����)
��2����ͼ2����D����ABC�ڲ��� ��E����ABC�ⲿ������BD�� CE�� ��BD��CE����������������ϵ��λ�ù�ϵ?��˵������.
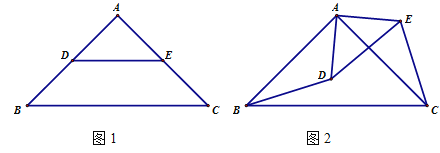
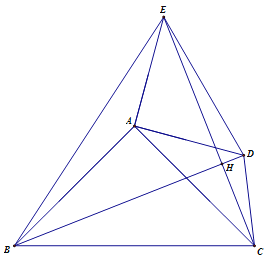
��3����ͼ3����D��E������ABC�ⲿ������BD�� CE�� CD�� EB��BD�� ��CE�ཻ��H��.
����BD=![]() �����ı���BCDE�������
�����ı���BCDE�������
����AB=3��AD=2����CD2=x��EB2=y����y��x֮��ĺ�����ϵʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�β����У�ijѧϰС��5��ѧ���ɼ����£���λ���֣���68 ��75��67��66��99.����ɼ���ƽ����![]() =____________��λ��M= ___________����ȥ��һ����߷ֺ��ƽ����
=____________��λ��M= ___________����ȥ��һ����߷ֺ��ƽ����![]() =_____________����ô�����
=_____________�������![]() ��M��
��M��![]() �����������У�����Ϊ��������С��ѧ����β���ɼ���һ��ˮƽ��������________________.
�����������У�����Ϊ��������С��ѧ����β���ɼ���һ��ˮƽ��������________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(a��b)2��(b��a)3��_________��(2m��n)3��(n��2m)2��______________;
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ����9-1=8����16-4=12����25-9=16����36-16=20����д����10����ʽ________________������n(n��1)��ʽ����________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ȥ������ȷ���ǣ�������
A. ��3��b��1������3b��3B. 2��2��a����4��a
C. ��3��b��1������3b+3D. 2��2��a����2a��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A. ��2a��2=2a2 B. a6��a3=a3 C. a3a2=a6 D. 3a2+2a3=5a5
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com