
【题目】如图,已知在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,
边上一点,![]() ,点
,点![]() 是射线
是射线![]() 上一点,联结
上一点,联结![]() 交射线
交射线![]() 于点
于点![]() ,
,

(1)求![]() 的长;
的长;
(2)若点![]() 在
在![]() 的延长线上,设
的延长线上,设![]() ,
,![]() ,求
,求![]() 与x之间的函数解析式,并写出定义域;
与x之间的函数解析式,并写出定义域;
(3)当![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的值为:
的值为:![]() 和
和![]() .
.
【解析】
(1)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,首先证明四边形ABMD是平行四边形,求出BM=AD=5,再证明△CMD是等边三角形,得到CM=CD=5,最后求出
,首先证明四边形ABMD是平行四边形,求出BM=AD=5,再证明△CMD是等边三角形,得到CM=CD=5,最后求出![]() 的长;
的长;
(2)延长![]() 交
交![]() 的延长线于点P,然后根据相似三角形的性质进行解答即可;
的延长线于点P,然后根据相似三角形的性质进行解答即可;
(3)利用当![]() 在
在![]() 的延长线上时,以及当
的延长线上时,以及当![]() 在线段
在线段![]() 上时,分别得出答案.
上时,分别得出答案.
(1)如图1所示,过点D作DM∥AB交BC于点M,
则四边形ABMD是平行四边形,
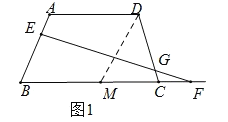
∴BM=AD=5,∠DMC=∠ABC=60°,
∵AD=AB=CD=5,
∴△CMD是等边三角形,
∴CM=CD=5,
∴BC=BM+CM=5+5=10;
(2)解:如图2,延长![]() 和
和![]() 相交于点
相交于点![]() ,
,
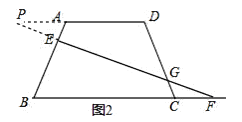
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,
![]()
![]() ,
,
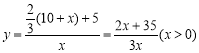 ;
;
(3)如图2,当![]() 在
在![]() 的延长线上时,
的延长线上时,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
如图3,当![]() 在线段
在线段![]() 上时,
上时,
![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
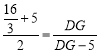 ,
,
![]() ,
,
综上所述![]() 的值为:
的值为:![]() 和
和![]() .
.



科目:初中数学 来源: 题型:
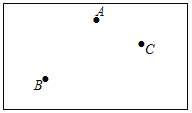
【题目】如图,盱眙县某校有一块矩形空地,在空地上的点A、B、C处种有三棵树,学校想在矩形的空地上建一个圆形花坛,使这三棵树帮在花坛的边上.
(1)请你帮学校把花坛的位置画出来(用直尺和圆规作图,保留作图痕迹):
(2)若AB=12m,AC=5m,∠BAC=90![]() ,求花坛的面积(结果保留
,求花坛的面积(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某隧道洞的内部截面顶部是抛物线形,现测得地面宽 AB=10m,隧道顶点O到地面AB的距离为5m,
(1)建立适当的平面直角坐标系,幵求该抛物线的解析式;
(2)一辆小轿车长 4.5米,宽2米,高1.5米,同样大小的小轿车通过该隧道,最多能有 几辆车幵行?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,滑动调节式遮阳伞的立柱![]() 垂直于地面
垂直于地面![]() ,
,![]() 为立柱上的滑动调节点,伞体的截面示意图为
为立柱上的滑动调节点,伞体的截面示意图为![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,
,![]() .当点
.当点![]() 位于初始位置
位于初始位置![]() 时,点
时,点![]() 与
与![]() 重合(图2).根据生活经验,当太阳光线与
重合(图2).根据生活经验,当太阳光线与![]() 垂直时,遮阳效果最佳.
垂直时,遮阳效果最佳.
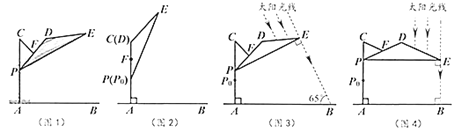
(1)上午10:00时,太阳光线与地面的夹角为![]() (图3),为使遮阳效果最佳,点
(图3),为使遮阳效果最佳,点![]() 需从
需从![]() 上调多少距离?(结果精确到
上调多少距离?(结果精确到![]() )
)
(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点![]() 在(1)的基础上还需上调多少距离?(结果精确到
在(1)的基础上还需上调多少距离?(结果精确到![]() )
)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
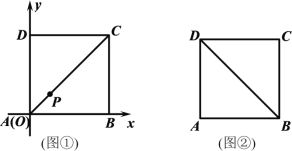
【题目】已知动点P在边长为1的正方形ABCD的内部,点P到边AD、AB的距离分别为m、n.
(1)以A为原点,以边AB所在直线为x轴,建立平面直角坐标系,如图①所示,当点P在对角线AC上,且m=![]() 时,求点P的坐标;
时,求点P的坐标;
(2)如图②,当m、n满足什么条件时,点P在△DAB的内部?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
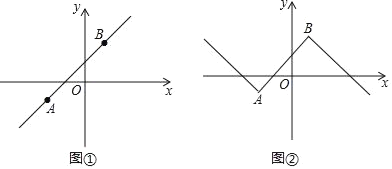
【题目】已知:在平面直角坐标系xOy中,点A(x1,y1)、B(x2,y2)是某函数图象上任意两点(x1<x2),将函数图象中x<x1的部分沿直线y=y1作轴对称,x>x2的部分沿直线y=y2作轴对称,与原函数图象中x1≤x≤x2的部分组成了一个新函数的图象,称这个新函数为原函数关于点A、B的“双对称函数”.例如:如图①,点A(﹣2,﹣1)、B(1,2)是一次函数y=x+1图象上的两个点,则函数y=x+1关于点A、B的“双对称函数”的图象如图②所示.
(1)点A(t,y1)、B(t+3,y2)是函数y=![]() 图象上的两点,y=
图象上的两点,y=![]() 关于点A、B的“双对称函数”的图象记作G,若G是中心对称图形,直接写出t的值.
关于点A、B的“双对称函数”的图象记作G,若G是中心对称图形,直接写出t的值.
(2)点P(![]() ,y1),Q(
,y1),Q(![]() +t,y2)是二次函数y=(x﹣t)2+2t图象上的两点,该二次函数关于点P、Q的“双对称函数”记作f.
+t,y2)是二次函数y=(x﹣t)2+2t图象上的两点,该二次函数关于点P、Q的“双对称函数”记作f.
①求P、Q两点的坐标(用含t的代数式表示).
②当t=﹣2时,求出函数f的解析式;
③若﹣1≤x≤1时,函数f的最小值为ymin,求﹣2≤ymin≤﹣1时,t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击选示在10次射击训练中的成绩统计图(部分)如图所示:

根据以上信息,请解答下面的问题;
选手 | A平均数 | 中位数 | 众数 | 方差 |
甲 | a | 8 | 8 | c |
乙 | 7.5 | b | 6和9 | 2.65 |
(1)补全甲选手10次成绩频数分布图.
(2)a= ,b= ,c= .
(3)教练根据两名选手手的10次成绩,决定选甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com