
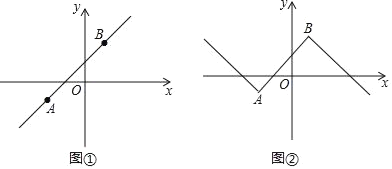
【题目】已知:在平面直角坐标系xOy中,点A(x1,y1)、B(x2,y2)是某函数图象上任意两点(x1<x2),将函数图象中x<x1的部分沿直线y=y1作轴对称,x>x2的部分沿直线y=y2作轴对称,与原函数图象中x1≤x≤x2的部分组成了一个新函数的图象,称这个新函数为原函数关于点A、B的“双对称函数”.例如:如图①,点A(﹣2,﹣1)、B(1,2)是一次函数y=x+1图象上的两个点,则函数y=x+1关于点A、B的“双对称函数”的图象如图②所示.
(1)点A(t,y1)、B(t+3,y2)是函数y=![]() 图象上的两点,y=
图象上的两点,y=![]() 关于点A、B的“双对称函数”的图象记作G,若G是中心对称图形,直接写出t的值.
关于点A、B的“双对称函数”的图象记作G,若G是中心对称图形,直接写出t的值.
(2)点P(![]() ,y1),Q(
,y1),Q(![]() +t,y2)是二次函数y=(x﹣t)2+2t图象上的两点,该二次函数关于点P、Q的“双对称函数”记作f.
+t,y2)是二次函数y=(x﹣t)2+2t图象上的两点,该二次函数关于点P、Q的“双对称函数”记作f.
①求P、Q两点的坐标(用含t的代数式表示).
②当t=﹣2时,求出函数f的解析式;
③若﹣1≤x≤1时,函数f的最小值为ymin,求﹣2≤ymin≤﹣1时,t的取值范围.
【答案】(1)t=![]() ;(2)①P(
;(2)①P(![]() ,t2+t+
,t2+t+![]() ),Q(
),Q(![]() +t,2t+
+t,2t+![]() );②y=
);②y=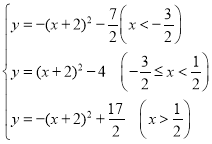 ;③﹣
;③﹣![]() ≤t≤
≤t≤![]() 或
或![]() ≤t≤
≤t≤![]()
【解析】
(1)根据定义、反比例函数图象性质和中心对称性质即可求出t;
(2)①直接代入计算即可;②新函数是分段函数,自变量x的范围分为x<![]() 或
或![]() ≤x≤
≤x≤![]() 或x>
或x>![]() ,二次函数图象翻折后开口方向与原来相反,顶点与原来顶点关于对称轴对称,可以先求新顶点;③分t≤-1,-1<t<0,t≥0进行讨论.
,二次函数图象翻折后开口方向与原来相反,顶点与原来顶点关于对称轴对称,可以先求新顶点;③分t≤-1,-1<t<0,t≥0进行讨论.
解:(1)如图1,

设点A(t,![]() ),A′(t+3,
),A′(t+3,![]() ),
),
∵G是中心对称图形,由反比例函数图象的中心对称性质可知:A与A′关于原点成中心对称,
∴t+t+3=0,解得:t=![]() ;
;
(2)①y1=![]() +2t=t2+t+
+2t=t2+t+![]() ,y2=
,y2=![]() +2t=2t+
+2t=2t+![]()
∴P(![]() ,t2+t+
,t2+t+![]() ),Q(
),Q(![]() +t,2t+
+t,2t+![]() ),
),
②当t=﹣2时,y=(x+2)2﹣4,P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),根据“双对称函数”定义可知:
),根据“双对称函数”定义可知:
新图象f由x<![]() 时抛物线y=(x+2)2﹣4沿直线y=
时抛物线y=(x+2)2﹣4沿直线y=![]() 翻折所得图象、x>
翻折所得图象、x>![]() 时抛物线y=(x+2)2﹣4沿直线y=
时抛物线y=(x+2)2﹣4沿直线y=![]() 翻折所得图象及
翻折所得图象及![]() ≤x≤
≤x≤![]() 时抛物线y=(x+2)2﹣4三个部分组成,
时抛物线y=(x+2)2﹣4三个部分组成,
∴当t=﹣2时,函数f的解析式为:y=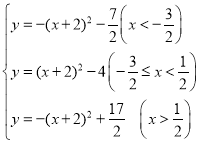
③∵当﹣1≤x≤1时,函数f的最小值为ymin,且﹣2≤ymin≤﹣1,
若t<0,该二次函数关于点P、Q的“双对称函数”为:y=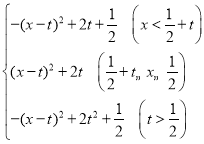 ,
,
当t≤﹣1时,点Q始终是“双对称函数”在﹣1≤x≤1的最低点,由﹣2≤2t+![]() ≤﹣1,∴
≤﹣1,∴![]() ≤t≤
≤t≤![]() ,故
,故![]() ≤t≤﹣1
≤t≤﹣1
当﹣1<t<0时,将x=﹣1代入得y=﹣(﹣1﹣t)2+2t+![]() =﹣t2
=﹣t2![]() ,由﹣2≤﹣t2
,由﹣2≤﹣t2![]() ≤﹣1,解得:
≤﹣1,解得:![]() ≤t≤
≤t≤![]() ,∴﹣1≤t≤
,∴﹣1≤t≤![]()
当t≥0时,由﹣2≤﹣(﹣1﹣t)2+2t2+![]() ≤﹣1,可解得:
≤﹣1,可解得:![]() ≤t≤
≤t≤![]() ,
,
综上所述,t的取值范围为:﹣![]() ≤t≤
≤t≤![]() 或
或![]() ≤t≤
≤t≤![]() ,
,


科目:初中数学 来源: 题型:
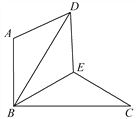
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,
边上一点,![]() ,点
,点![]() 是射线
是射线![]() 上一点,联结
上一点,联结![]() 交射线
交射线![]() 于点
于点![]() ,
,

(1)求![]() 的长;
的长;
(2)若点![]() 在
在![]() 的延长线上,设
的延长线上,设![]() ,
,![]() ,求
,求![]() 与x之间的函数解析式,并写出定义域;
与x之间的函数解析式,并写出定义域;
(3)当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
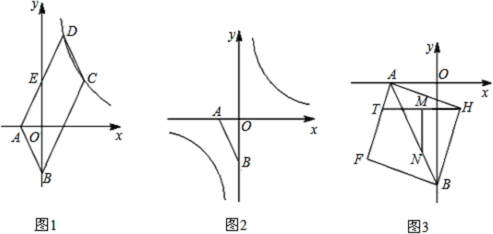
【题目】如图1,已知点![]() ,
,![]() ,且
,且![]() 、
、![]() 满足
满足![]() ,
,![]() 的边
的边![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() 为
为![]() 中点,双曲线
中点,双曲线![]() 经过
经过![]() 、
、![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 在
在![]() 轴上,若以点
轴上,若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,试求满足要求的所有点
为顶点的四边形是平行四边形,试求满足要求的所有点![]() 、
、![]() 的坐标;
的坐标;
(3)以线段![]() 为对角线作正方形
为对角线作正方形![]() (如图
(如图![]() ,点
,点![]() 是边
是边![]() 上一动点,
上一动点,![]() 是
是![]() 的中点,
的中点,![]() ,交
,交![]() 于
于![]() ,当
,当![]() 在
在![]() 上运动时,
上运动时,![]() 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某地区中学生一周课外阅读时长的情况,随机抽取部分中学生进行调查,根据调查结果,将阅读时长分为四类:2小时以内,2~4小时(含2小时),4~6小时(含4小时),6小时及以上,并绘制了如图所示尚不完整的统计图.
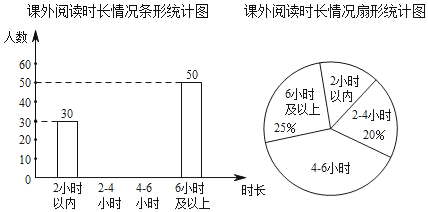
(1)本次调查共随机抽取了 名中学生,其中课外阅读时长“2~4小时”的有 人;
(2)扇形统计图中,课外阅读时长“4~6小时”对应的圆心角度数为 °;
(3)若该地区共有20000名中学生,估计该地区中学生一周课外阅读时长不少于4小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B两地.甲、乙两人同时出发,甲骑电动车从A地到B地,中途出现故障后停车维修,修好车后以原速继续行驶到B地;乙骑摩托车从B地到A地,到达A地后立即按原原速返回,结果两人同时到B地.如图是甲、乙两人与B地的距离y(km)与乙行驶时间x(h)之间的函数图象.
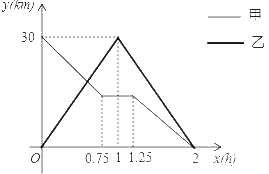
(1)A、B两地间的距离为 km;
(2)求乙与B地的距离y(km)与乙行驶时间x(h)之间的函数关系式;
(3)求甲、乙第一次相遇的时间;
(4)若两人之间的距离不超过10km时,能够用无线对讲机保持联系,请求出乙在行进中能用无线对讲机与甲保持联系的x取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行以“助人为乐,乐在其中”为主题的演讲比赛,比赛设一个第一名,一个第二名,两个并列第三名.前四名中七、八年级各有一名同学,九年级有两名同学,小蒙同学认为前两名是九年级同学的概率是![]() ,你赞成他的观点吗?请用列表法或画树形图法分析说明.
,你赞成他的观点吗?请用列表法或画树形图法分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一个六面分别标有数字1,2,3,4,5,6,且质地均匀的正方体筛子,另有三张正面分别标有1,2,3,的卡片(卡片除数字外,其他都相同),先由小明掷筛子一次,记下筛子向上一面出现的数字,然后由小王从三张背面朝上放置在桌面上的卡片中随机抽取一张,记下卡片上的数字。
(1)请用列表或树状图的方法,求出筛子向上一面出现的数字与卡片上的数字之积为6的概率;
(2)小明和小王做游戏,约定游戏规则如下:若筛子向上一面出现的数字与卡片上的数字之积大于7,则小明赢;若筛子向上一面出现的数字与卡片上的数字之积小于7,则小王赢;问小明和小王谁赢的可能性更大?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 是
是![]() 上一点,
上一点,![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 于点
于点![]() ,与
,与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() 平分
平分![]() ,连接
,连接![]() ,
,![]() .
.
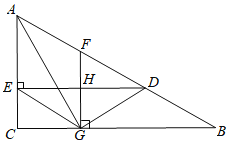
(1)求证:![]() ;
;
(2)小亮同学经过探究发现:![]() .请你帮助小亮同学证明这一结论.
.请你帮助小亮同学证明这一结论.
(3)若![]() ,判定四边形
,判定四边形![]() 是否为菱形,并说明理由.
是否为菱形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com