
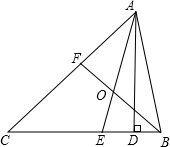
 如图,△ABC中,AE、BF是角平分线,它们相交于点O.(∠ABC>∠C),
如图,△ABC中,AE、BF是角平分线,它们相交于点O.(∠ABC>∠C), ∠C;
∠C; (∠CAB+∠CBA),
(∠CAB+∠CBA), (180°-∠C)
(180°-∠C) ∠C;
∠C; (∠ABC-∠C).
(∠ABC-∠C). (180°-∠C-∠ABC),
(180°-∠C-∠ABC), (180°-∠C-∠ABC)],
(180°-∠C-∠ABC)], (∠ABC-∠C).
(∠ABC-∠C). (∠CAB+∠CBA),以及∠CAB+∠CBA=180°-∠C,即可得出∠BOA=180°-
(∠CAB+∠CBA),以及∠CAB+∠CBA=180°-∠C,即可得出∠BOA=180°- (180°-∠C)整理得出即可;
(180°-∠C)整理得出即可; (180°-∠C-∠ABC),然后利用三角形外角性质,可先求∠AED,再次利用三角形外角性质,容易求出∠DAE即可.
(180°-∠C-∠ABC),然后利用三角形外角性质,可先求∠AED,再次利用三角形外角性质,容易求出∠DAE即可.

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com