
【题目】已知如图,矩形OABC放置于平面直角坐标系中,点O与原点重合,点A在x轴正半轴上,点C在y轴正半轴上,点B的坐标为(6,3),点D是边BC上的一动点,连接OD,作点C关于直线OD的对称点C′.
(1)若点C、C′、A在一直线上时,求点D的坐标;
(2)若点C′到矩形两对边所在直线距离之比为1:2时,求点C′的坐标;
(3)若连接BC′,则线段BC′的长度范围是 .

【答案】(1)D(![]() ,3);(2)点C′的坐标为(
,3);(2)点C′的坐标为(![]() ,2)或(2
,2)或(2![]() ,1);(3)3
,1);(3)3![]() ﹣3≤BC′≤6.
﹣3≤BC′≤6.
【解析】试题分析:(1)根据轴对称的性质和矩形的性质易证∠DCE=∠COD,再求得CD的长,即可得点D的坐标;(2)分点C′到矩形OA边与BC边的距离之比为1:2和点C′到矩形BC边与OA边的距离之比为2:1两种情况求点C′的坐标即可;(3)由OC′=OC,可知点C′在以O为圆心,以3为半径的弧上(如图).当点D与点C或点B重合时,BC′有最大值.当点C′在直线OB上时,BC′有最小值.由此即可求得BC的取值范围.
试题解析:
(1)如下图所示:

∵点C、C′、A在一直线上,
∴tan∠BCC′=![]() =
=![]() .
.
∵点C与点C′关于OD对称,
∴OD⊥CC′.
∴∠DCE+∠CDE=90°.
∵∠CDE+∠COD=90°.
∴∠DCE=∠COD.
∴tan∠COD=![]() =
=![]() ,
,
∴CD=![]() OC=
OC=![]() .
.
∴D(![]() ,3).
,3).
(2)设点C′的坐标为(x,y).
由轴对称的性质可知OC=OC′=3.
由两点间的距离公式可知x2+y2=9.
点C′到矩形两对边所在直线距离之比为1:2时,
C′的纵坐标为2或1.
将y=2代入x2+y2=9得:x2+4=9,解得:x=![]() 或x=﹣
或x=﹣![]() (舍去),
(舍去),
∴C′(![]() ,2).
,2).
将y=1代入x2+y2=9得:x2+1=9,解得:x=2![]() 或x=﹣2
或x=﹣2![]() (舍去),
(舍去),
∴C′(2![]() ,1).
,1).
综上所述,点C′的坐标为(![]() ,2)或(2
,2)或(2![]() ,1).
,1).
(3)∵OC′=OC,
∴点C′在以O为圆心,以3为半径的弧上.
如下图所示:

当点D与点C或点B重合时,BC′有最大值,最大值=BD=6.
当点C′在直线OB上时,BC′有最小值.
在△ABO中,依据勾股定理可知OB=![]() =3
=3![]() .
.
∵OC′=OC=3,
∴BC′的最小值=BO﹣OC′=3![]() ﹣3.
﹣3.
∴线段BC′的长度范围是3![]() ﹣3≤BC′≤6.
﹣3≤BC′≤6.
故答案为:3![]() ﹣3≤BC′≤6.
﹣3≤BC′≤6.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,图中直线表示三条相互交叉的路,现要建一个货运中转站,要求它到三条公路的距离相等,则选择的地址有( )

A. 4处B. 3处C. 2处D. 1处
查看答案和解析>>
科目:初中数学 来源: 题型:
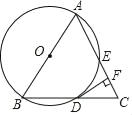
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,过点D作⊙O的切线与AC交于点F.
(1)求证:EF=CF;
(2)若AE=8,cosA=![]() ,求DF的长.
,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y﹣2与x成正比例,当x=2时,y=6.
(1)求y与x之间的函数解析式.
(2)在所给直角坐标系中画出函数图象.
(3)由函数图象直接写出当﹣2≤y≤2时,自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线y=x+b与双曲线y=![]() (x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.
(x<0)交于点A(﹣1,﹣5),并分别与x轴、y轴交于点C、B.
(1)求出b、m的值;
(2)点D在x轴的正半轴上,若以点D、C、B组成的三角形与△OAB相似,试求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
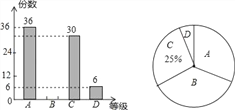
【题目】四川省第十三届运动会将于2018年8月在我市举行,某校组织了主题“我是运动会志愿者”的电子小报作品征集活动,先从中随机抽取了部分作品,按A,B,C,D四个等级评分,然后根据统计结果绘制了如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
(1)求此次抽取的作品中等级为B的作品数,并补全条形统计图;
(2)求扇形统计图为D的扇形圆心角的度数;
(3)该校计划从抽取的这些作品中选取部分作品参加市区的作品展.已知其中所选的到市区参展的A作品比B作品少4份,且A、B两类作品数量和正好是本次抽取的四个等级作品数量的![]() ,求选取到市区参展的B类作品有多少份.
,求选取到市区参展的B类作品有多少份.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长都为a的正方形内分别排列着一些大小相等的圆.

(1)根据图中的规律,第4个正方形内圆的个数是 ,第n个正方形内圆的个数是 .
(2)如果把正方形内除去圆的部分都涂上阴影.
①用含a的代数式分别表示第1个正方形中和第3个正方形中阴影部分的面积.(结果保留π)
②若a=10,请直接写出第2014个正方形中阴影部分的面积 .(结果保留π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com