
【题目】如图,在边长都为a的正方形内分别排列着一些大小相等的圆.

(1)根据图中的规律,第4个正方形内圆的个数是 ,第n个正方形内圆的个数是 .
(2)如果把正方形内除去圆的部分都涂上阴影.
①用含a的代数式分别表示第1个正方形中和第3个正方形中阴影部分的面积.(结果保留π)
②若a=10,请直接写出第2014个正方形中阴影部分的面积 .(结果保留π)
【答案】(1)16,n2个;(2)①第一个![]() a2;第三个
a2;第三个![]() a2;②100﹣25π.
a2;②100﹣25π.
【解析】
(1)先根据题中已知的三个图形找到其中的规律,即可得出答案;
(2)①利用阴影部分的面积等于正方形面积减去圆的面积即可得出答案;
②从①中找到阴影部分面积存在的规律,利用规律即可求出答案.
解:(1)图形①圆的个数是1,
图形②圆的个数是4,
图形③圆的个数是9,
图形④圆的个数是16,
…;
第n个正方形中圆的个数为n2个;
(2)①第一个S阴影=a2﹣π(![]() )2=
)2=![]() a2;
a2;
第二个S阴影=a2﹣4π(![]() )2=
)2=![]() a2;
a2;
第三个S阴影=a2﹣9π(![]() )2=
)2=![]() a2;
a2;
②从以上计算看出三个图形中阴影部分的面积均相等,与圆的个数无关.
第n图形中阴影部分的面积是S阴影=a2﹣n2π(![]() )2=
)2=![]() a2;
a2;
当a=10,第2014个阴影部分的面积为![]() ×102=100﹣25π.
×102=100﹣25π.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】已知如图,矩形OABC放置于平面直角坐标系中,点O与原点重合,点A在x轴正半轴上,点C在y轴正半轴上,点B的坐标为(6,3),点D是边BC上的一动点,连接OD,作点C关于直线OD的对称点C′.
(1)若点C、C′、A在一直线上时,求点D的坐标;
(2)若点C′到矩形两对边所在直线距离之比为1:2时,求点C′的坐标;
(3)若连接BC′,则线段BC′的长度范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形 AEF 的顶点 E 在等腰直角三角形 ABC 的边 BC上.AB 的延长线交 EF 于 D 点,其中∠AEF=∠ABC=90°.
(1)求证:![]()
(2)若 E 为 BC 的中点,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-2x+6与x轴交于点A,与直线y=x交于点B.
(1)点A坐标为_____________.
(2)动点M从原点O出发,以每秒1个单位长度的速度沿着O→A的路线向终点A匀速运动,过点M作MP⊥x轴交直线y=x于点P,然后以MP为直角边向右作等腰直角△MPN.设运动t秒时,ΔMPN与ΔOAB重叠部分的面积为S.求S与t之间的函数关系式,并直接写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某苹果生产基地,用30名工人进行采摘或加工苹果,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售,另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利4 000元,加工成罐头出售每吨获利10 000元.采摘的工人每人可以采摘苹果0.4吨,加工罐头的工人每人可加工苹果0.3吨.采摘的苹果一部分用于加工罐头,其余直接出售.设有x名工人进行苹果采摘,罐头和苹果全部售出后,总利润为y元.
(1)加工成罐头的苹果数量为 吨,直接出售的苹果数量为 吨.(用含x的代数式表示)
(2)求y与x之间的函数关系式,并求出自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
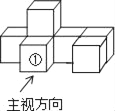
A. 主视图改变,俯视图改变 B. 左视图改变,俯视图改变
C. 俯视图不变,左视图改变 D. 主视图不变,左视图不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂以80元/箱的价格购进60箱原材料,准备由甲、乙两车间全部用于生产A产品.甲车间用每箱原材料可生产出A产品12千克,需耗水4吨;乙车间通过节能改造,用每箱原材料可生产出的A产品比甲车间少2千克,但耗水量是甲车间的一半.已知A产品售价为30元/千克,水价为5元/吨.设甲车间用x箱原材料生产A产品.
(1)用含x的代数式表示:乙车间用________箱原材料生产A产品;
(2)求两车间生产这批A产品的总耗水量;
(3)若两车间生产这批产品的总耗水为200吨,则该厂如何分配两车间的生产原材料?
(4)用含x的代数式表示这次生产所能获取的利润并化简.(注:利润=产品总售价-购买原材料成本-水费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图1,△ABC中,∠ACB=90°,AC=BC,MN是过点A的直线,DB⊥MN于点D,联结CD.求证:BD+AD=![]() CD.
CD.
小明的思考过程如下:要证BD+AD=![]() CD,需要将BD,AD转化到同一条直线上,可以在MN上截取AE=BD,并联结EC,可证△ACE和△BCD全等,得到CE=CD,且∠ACE=∠BCD,由此推出△CDE为等腰直角三角形,可知DE=
CD,需要将BD,AD转化到同一条直线上,可以在MN上截取AE=BD,并联结EC,可证△ACE和△BCD全等,得到CE=CD,且∠ACE=∠BCD,由此推出△CDE为等腰直角三角形,可知DE=![]() CD,于是结论得证。
CD,于是结论得证。
小聪的思考过程如下:要证BD+AD=![]() CD,需要构造以CD为腰的等腰直角三角形,可以过点C作CE⊥CD交MN于点E,可证△ACE和△BCD全等,得到CE=CD,且AE=BD,由此推出△CDE为等腰直角三角形,可知DE=
CD,需要构造以CD为腰的等腰直角三角形,可以过点C作CE⊥CD交MN于点E,可证△ACE和△BCD全等,得到CE=CD,且AE=BD,由此推出△CDE为等腰直角三角形,可知DE=![]() CD,于是结论得证。
CD,于是结论得证。
请你参考小明或小聪的思考过程解决下面的问题:
(1)将图1中的直线MN绕点A旋转到图2和图3的两种位置时,其它条件不变,猜想BD,AD,CD之间的数量关系,并选择其中一个图形加以证明;
(2)在直线MN绕点A旋转的过程中,当∠BCD=30°,BD=![]() 时,CD=___.
时,CD=___.

查看答案和解析>>
科目:初中数学 来源: 题型:
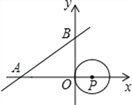
【题目】如图,直线y=![]() x+
x+![]() 与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左平移,当⊙P与该直线相切时,点P坐标为___.
与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左平移,当⊙P与该直线相切时,点P坐标为___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com