
【题目】如图,等腰直角三角形 AEF 的顶点 E 在等腰直角三角形 ABC 的边 BC上.AB 的延长线交 EF 于 D 点,其中∠AEF=∠ABC=90°.
(1)求证:![]()
(2)若 E 为 BC 的中点,求![]() 的值.
的值.

【答案】(1)见解析;(2)![]()
【解析】
(1)由△AEF、△ABC是等腰直角三角形,易证得△FAD∽△CAE,然后由相似三角形的对应边成比例,可得![]() ,又由等腰直角三角形的性质,可得AF=
,又由等腰直角三角形的性质,可得AF=![]() AE,即可证得
AE,即可证得![]() ;
;
(2)首先设BE=a,由射影定理,可求得DB的长,继而可求得DA的长,即可求得答案.
(1)证明:∵△AEF、△ABC是等腰直角三角形,
∴∠EAF=∠BAC=45°,∠F=∠C=45°,
∴∠FAD=∠CAE,
∴△FAD∽△CAE,
∴![]() ,
,
∵∠AEF=90°,AE=EF,
∴AF=![]() AE,
AE,
∴![]() ;
;
(2)设BE=a,
∵E为BC的中点,
∴EC=BE=a,AB=BC=2a,
∵∠AEF=∠ABC=90°,
∴BE![]() =ABDB,
=ABDB,
∴DB=![]() ,
,
∵DA=DB+AB,
∴DA=![]() ,
,
∴![]() =
=![]() .
.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
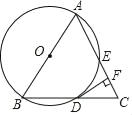
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,过点D作⊙O的切线与AC交于点F.
(1)求证:EF=CF;
(2)若AE=8,cosA=![]() ,求DF的长.
,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
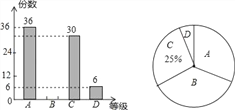
【题目】四川省第十三届运动会将于2018年8月在我市举行,某校组织了主题“我是运动会志愿者”的电子小报作品征集活动,先从中随机抽取了部分作品,按A,B,C,D四个等级评分,然后根据统计结果绘制了如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
(1)求此次抽取的作品中等级为B的作品数,并补全条形统计图;
(2)求扇形统计图为D的扇形圆心角的度数;
(3)该校计划从抽取的这些作品中选取部分作品参加市区的作品展.已知其中所选的到市区参展的A作品比B作品少4份,且A、B两类作品数量和正好是本次抽取的四个等级作品数量的![]() ,求选取到市区参展的B类作品有多少份.
,求选取到市区参展的B类作品有多少份.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随时用的共享单车。某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费。具体收费标准如下:

同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:

(1)写出a、b的值。
(2)已知该校有5100名师生,且A品牌共享单车投放该校一天的费用为5800元。试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点C在线段AB上,若BC=![]() AC,则称点C是线段AB的一个圆周率点.
AC,则称点C是线段AB的一个圆周率点.
如图,已知点C是线段AB的一个靠近点A的圆周率点,AC=3.
(1)AB= ;(结果用含![]() 的代数式表示)
的代数式表示)
(2)若点D是线段AB的另一个圆周率点(不同于点C),则CD= ;
(3)若点E在线段AB的延长线上,且点B是线段CE的一个圆周率点.求出BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1,第2次将点A1向右平移6个单位长度到达点A2,第3次将点A2向左移动9个单位长度到达点A3…则第6次移动到点A6时,点A6在数轴上对应的实数是_____;按照这种规律移动下去,至少移动_____次后该点到原点的距离不小于41.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长都为a的正方形内分别排列着一些大小相等的圆.

(1)根据图中的规律,第4个正方形内圆的个数是 ,第n个正方形内圆的个数是 .
(2)如果把正方形内除去圆的部分都涂上阴影.
①用含a的代数式分别表示第1个正方形中和第3个正方形中阴影部分的面积.(结果保留π)
②若a=10,请直接写出第2014个正方形中阴影部分的面积 .(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题
(1)如图1,已知点A、B、C,直线l及l上一点M,请你按照下列要求画出图形.
①画射线BM
②画线段AC
③请在直线l上确定一点O,使点O到点A与点B的距离之和(OA+OB)最小
(2)有5个大小一样的正方形制成的如图2所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(只需添加一个符合要求的正方形即可,并用阴影表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com